
| A. | $\frac{{2\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{33}}}{3}$ | C. | $\frac{{4\sqrt{6}}}{3}$ | D. | $\frac{{2\sqrt{33}}}{3}$ |
分析 由圆周角定理及球的性质可判断PA为球的直径,利用余弦定理求出PA与平面ABC所成角的大小,即可得出球心到平面ABC的距离.
解答 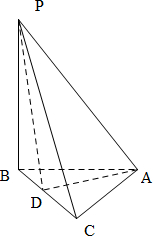 解:∵∠PBA=∠PCA=90°,
解:∵∠PBA=∠PCA=90°,
∴PA为平面PAB所在圆的截面的直径,
同理PA也是PBC所在圆的截面的直径,
∴PA的中点为外接球的球心,
由勾股定理得PB=PC=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
取BC的中点D,连接AD,
则∠PAD为PA与平面ABC所成的角,
经计算得AD=$\sqrt{3}$,PD=$\sqrt{11}$,
∴cos∠PAD=$\frac{16+3-11}{2×4×\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴sin∠PAD=$\frac{\sqrt{6}}{3}$,
∴球心O到平面ABC的距离d=$\frac{1}{2}$PAsin∠PAD=$\frac{2\sqrt{6}}{3}$.
故选A.
点评 本题考查了棱锥的结构特征,棱锥与外接球的关系,属于中档题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{8}{5}}]∪[{3,+∞})$ | B. | $[{-1,\frac{1}{7}}]$ | C. | (-1,0]∪[3,+∞) | D. | (-∞,-1]∪[7,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{3}{2}$,2$\sqrt{3}$) | B. | (2,2$\sqrt{3}$) | C. | (1,2) | D. | (1,2$\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | ±1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com