
分析 (Ⅰ)$f(x)=|{x+a+1}|+|{x-\frac{4}{a}}|≥|{(x+a+1)-(x-\frac{4}{a})}|=|{a+1+\frac{4}{a}}|$≥5;
(Ⅱ)由f(1)<6得$|{1-\frac{4}{a}}|<4-a$,$\frac{{|{a-4}|}}{a}<4-a$,
分①当a≥4,②当a<4 求实数a的取值范围.
解答 解:(Ⅰ)证明:$f(x)=|{x+a+1}|+|{x-\frac{4}{a}}|≥|{(x+a+1)-(x-\frac{4}{a})}|=|{a+1+\frac{4}{a}}|$
∵a>0,∴$f(x)≥a+1+\frac{4}{a}≥2\sqrt{a•\frac{4}{a}}+1=5$….(5分)
(Ⅱ)由f(1)<6得:$|{a+2}|+|{1-\frac{4}{a}}|<6$,
∵a>0,∴$|{1-\frac{4}{a}}|<4-a$,$\frac{{|{a-4}|}}{a}<4-a$…(7分)
①当a≥4时,不等式$\frac{{|{a-4}|}}{a}<4-a$无解;
②当a<4时,不等式$\frac{{|{a-4}|}}{a}<4-a$,即$\frac{1}{a}<1$,a>1,
所以1<a<4…(9分)
综上,实数a的取值范围是(1,4)…(10分)
点评 本题考查了绝对值不等式的性质,解绝对值不等式,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 17 | C. | 28 | D. | 41 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
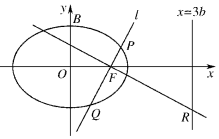 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),点F,B分别是椭圆的右焦点与上顶点,O为坐标原点,记△OBF的周长与面积分别为C和S.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),点F,B分别是椭圆的右焦点与上顶点,O为坐标原点,记△OBF的周长与面积分别为C和S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{33}}}{3}$ | C. | $\frac{{4\sqrt{6}}}{3}$ | D. | $\frac{{2\sqrt{33}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
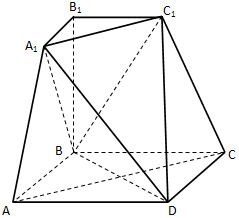 如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.
如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0>2,${2^{x_0}}-3≤0$ | B. | ?x≤2,2x-3>0 | C. | ?x>2,2x-3≤0 | D. | ?x0>2,${2^{x_0}}-3>0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com