
| A. | $[{\frac{π}{12},\frac{π}{4}}]$ | B. | $[{\frac{π}{6},\frac{5π}{12}})$ | C. | $[{\frac{π}{6},\frac{π}{3}}]$ | D. | $({\frac{π}{6},\frac{π}{4}}]$ |
分析 利用函数y=Asin(ωx+φ)的图象变换规律,求出g(x)的解析式,函数g(x)在区间$[{0,\frac{π}{3}}]$上单调递增,且函数g(x)的最大负零点在区间$({-\frac{π}{3},-\frac{π}{12}})$内,根据三角函数的性质建立不等式,可得结论.
解答 解:函数f(x)=sin2x的图象向右平移ϕ,可得g(x)=sin(2x-2ϕ),
函数g(x)在区间$[{0,\frac{π}{3}}]$上单调递增吗,
可得:$\left\{\begin{array}{l}{-2ϕ≥-\frac{π}{2}+2kπ}\\{\frac{2π}{3}-2ϕ≤\frac{π}{2}+2kπ}\end{array}\right.$,k∈Z,可得:$-kπ+\frac{π}{12}≤ϕ≤-kπ+\frac{π}{4}$,
∵0<φ<$\frac{π}{2}$,
∴$\frac{π}{12}$≤ϕ$≤\frac{π}{4}$.
函数g(x)的零点为2x-2ϕ=kπ,k∈Z,即x=$\frac{1}{2}kπ+ϕ$
最大负零点在区间$({-\frac{π}{3},-\frac{π}{12}})$内,
可得:${-\frac{π}{3}<\frac{1}{2}kπ+ϕ<-\frac{π}{12}}\end{array}\right.$,k∈Z,即$-\frac{1}{2}kπ-\frac{π}{3}<$ϕ$<-\frac{1}{2}kπ-\frac{π}{12}$
∵0<φ<$\frac{π}{2}$,
∴$\frac{π}{6}$<ϕ$<\frac{5π}{12}$
综上可得ϕ的取值范围是($\frac{π}{6}$,$\frac{π}{4}$].
故选D.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | p1∧p2 | B. | p1∨p2 | C. | p1∧(¬p2) | D. | (¬p1)∨p2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{2,\sqrt{3}+1}]$ | B. | $[{2,2\sqrt{3}+1}]$ | C. | $[{\sqrt{2},2}]$ | D. | $[{\sqrt{2},\sqrt{3}+1}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
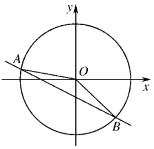 如图,直线x+2y=a与圆x2+y2=1相交于不同的两点A(x1,y1),B(x2,y2),O为坐标原点,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=a,则实数a的值为( )
如图,直线x+2y=a与圆x2+y2=1相交于不同的两点A(x1,y1),B(x2,y2),O为坐标原点,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=a,则实数a的值为( )| A. | $\frac{5-\sqrt{65}}{4}$ | B. | $\frac{\sqrt{65}-5}{4}$ | C. | $\frac{5-\sqrt{55}}{4}$ | D. | $\frac{\sqrt{55}-5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
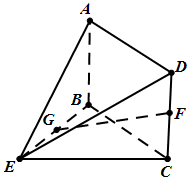 如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BCE,BE⊥CE,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BCE,BE⊥CE,AB=BE=EC=2,G,F分别是线段BE,DC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
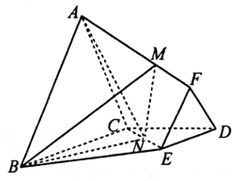 如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为CE中点,$\overrightarrow{AM}=λ\overrightarrow{AF}({λ∈R,λ>0})$.
如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为CE中点,$\overrightarrow{AM}=λ\overrightarrow{AF}({λ∈R,λ>0})$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com