
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
分析 直线过抛物线的焦点F(1,0),把直线方程代入抛物线的方程解得A、B 的坐标,由$\overrightarrow{OF}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$,得到3λ+$\frac{1}{3}$μ=1,2$\sqrt{3}$λ-$\frac{2\sqrt{3}}{3}$μ=0,解方程从而求得λ-μ的值.
解答 解:直线$\sqrt{3}x-y-\sqrt{3}=0$过抛物线的焦点F(1,0),
把直线方程代入抛物线的方程y2=4x,解得$\left\{\begin{array}{l}{x=3}\\{y=2\sqrt{3}}\end{array}\right.$,或$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=-\frac{2\sqrt{3}}{3}}\end{array}\right.$,
不妨设A(3,2$\sqrt{3}$)、B ($\frac{1}{3}$,-$\frac{2\sqrt{3}}{3}$).
∵$\overrightarrow{OF}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$,
∴(1,0)=(3λ,2$\sqrt{3}$λ)+($\frac{1}{3}$μ,-$\frac{2\sqrt{3}}{3}$μ)
=(3λ+$\frac{1}{3}$μ,2$\sqrt{3}$λ-$\frac{2\sqrt{3}}{3}$μ ).
∴3λ+$\frac{1}{3}$μ=1,2$\sqrt{3}$λ-$\frac{2\sqrt{3}}{3}$μ=0,
∴λ=$\frac{1}{4}$,μ=$\frac{3}{4}$,
则λ-μ=-$\frac{1}{2}$.
故选:B.
点评 本题考查两个向量坐标形式的运算,直线和抛物线的位置关系,由$\overrightarrow{OF}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$得到λ、μ的方程是解题的关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:解答题
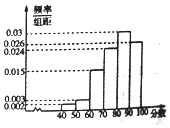 2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图:
2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{10}$ | C. | $\sqrt{11}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -112 | B. | -56 | C. | 112 | D. | 56 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| A | B | 合计 | |
| 认可 | |||
| 不认可 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1≤x≤2} | B. | (1,2) | C. | {1,2} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=sin({\frac{x}{2}+\frac{π}{6}})$ | B. | $y=cos({\frac{x}{2}-\frac{π}{6}})$ | C. | $y=cos({2x+\frac{π}{6}})$ | D. | $y=sin({2x-\frac{π}{6}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(0,$\frac{1}{2}$) | B. | (-∞,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,+∞) | D. | (0,$\frac{1}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com