
| A. | [-$\frac{2}{{e}^{2}}$,0) | B. | [-$\frac{2}{{e}^{2}}$,0)∪{$-\frac{1}{2}$e} | C. | [-$\frac{e}{2}$,0) | D. | [-$\frac{2}{{e}^{2}}$,0] |
分析 分类参数得-a=$\frac{lnx+1}{{x}^{2}}$,判断右侧函数的单调性,作出函数图象,根据方程只有1解得出a的范围.
解答 解:令f(x)=0得-a=$\frac{lnx+1}{{x}^{2}}$,
令g(x)=$\frac{lnx+1}{{x}^{2}}$,则g′(x)=$\frac{\frac{1}{x}•{x}^{2}-(lnx+1)•2x}{{x}^{4}}$=$\frac{-2lnx-1}{{x}^{3}}$,
令g′(x)=0得x=e${\;}^{-\frac{1}{2}}$,
∴当x∈($\frac{1}{e}$,e${\;}^{-\frac{1}{2}}$)时,g′(x)>0,当x∈(e${\;}^{-\frac{1}{2}}$,e)时,g′(x)<0,
∴g(x)在($\frac{1}{e}$,e${\;}^{-\frac{1}{2}}$)上单调递增,在(e${\;}^{-\frac{1}{2}}$,e)上单调递减,
且g($\frac{1}{e}$)=0,g(e)=$\frac{2}{{e}^{2}}$,g(e${\;}^{-\frac{1}{2}}$)=$\frac{e}{2}$.
作出g(x)的大致函数图象如图所示:
∵f(x)在($\frac{1}{e}$,e)上只有一个零点,∴-a=g(x)在($\frac{1}{e}$,e)上只有1解,
∴0<-a≤$\frac{2}{{e}^{2}}$或-a=$\frac{e}{2}$,解得-$\frac{2}{{e}^{2}}$≤a<0或a=-$\frac{e}{2}$.
故选B.
点评 本题考查了方程零点个数与函数图象的关系,函数的单调性判断,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
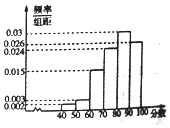 2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图:
2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\sqrt{2},+∞})$ | B. | $[{\sqrt{2},+∞})$ | C. | $({1,\sqrt{2}})$ | D. | $({1,\sqrt{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{10}$ | C. | $\sqrt{11}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=sin({\frac{x}{2}+\frac{π}{6}})$ | B. | $y=cos({\frac{x}{2}-\frac{π}{6}})$ | C. | $y=cos({2x+\frac{π}{6}})$ | D. | $y=sin({2x-\frac{π}{6}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com