
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用定积分求解判断(1);由两直线垂直与系数的关系求出m值判断(2);求出P(ξ>2)=0.1判断(3);根据两圆相交判断(4).
解答 解:(1)由f(a)=${∫}_{0}^{a}$cos xdx=sina,可得f($\frac{π}{2}$)=sin$\frac{π}{2}$=1,故(1)正确;
(2)直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0互相垂直?(m+2)(m-2)+m(m+2)=0,即m=-2或m=1.
∴“m=-2”是“直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0互相垂直”的充分不必要条件,故(2)错误;
(3)随机变量ξ服从正态分布N(0,δ2),且P(-2≤ξ≤0)=0.4,则P(ξ>2)=0.1,故(3)错误;
(4)圆C1:x2+y2+2x=0化为(x+1)2+y2=1,圆C2:x2+y2-1=0化为x2+y2=1,两圆的圆心距d=1,小于两半径之和,两圆相交,
∴这两个圆恰有两条公切线,故(4)正确.
∴正确的命题是2个.
故选:B.
点评 本题考查命题的真假判断与应用,考查直线与圆的位置关系,训练了定积分及正态分布概率的求法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $({\sqrt{2},+∞})$ | B. | $[{\sqrt{2},+∞})$ | C. | $({1,\sqrt{2}})$ | D. | $({1,\sqrt{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{10}$ | C. | $\sqrt{11}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -112 | B. | -56 | C. | 112 | D. | 56 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1≤x≤2} | B. | (1,2) | C. | {1,2} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
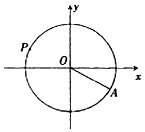 水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为R的水车,一个水斗从点A(3$\sqrt{3}$,-3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t秒后,水斗旋转到P点,设P的坐标为(x,y),其纵坐标满足y=f(t)=Rsin(ωt+φ)(t≥0,ω>0,|φ|<$\frac{π}{2}}$).则下列叙述错误的是( )
水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为R的水车,一个水斗从点A(3$\sqrt{3}$,-3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t秒后,水斗旋转到P点,设P的坐标为(x,y),其纵坐标满足y=f(t)=Rsin(ωt+φ)(t≥0,ω>0,|φ|<$\frac{π}{2}}$).则下列叙述错误的是( )| A. | $R=6,ω=\frac{π}{30},φ=-\frac{π}{6}$ | |
| B. | 当t∈[35,55]时,点P到x轴的距离的最大值为6 | |
| C. | 当t∈[10,25]时,函数y=f(t)单调递减 | |
| D. | 当t=20时,$|{PA}|=6\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com