
| 机床甲 | 10 | 9.8 | 10 | 10.2 |
| 机床乙 | 10.1 | 10 | 9.9 | 10 |
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 (件)与月平均气温
(件)与月平均气温 (℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:月平均气温 (℃) (℃) | 17 | 13 | 8 | 2 |
月销售量 (件) (件) | 24 | 33 | 40 | 55 |
 中的
中的 ,气象部门预测下个月的平均气温约为6℃,据此估计,该商场下月毛衣的销售量约为 件。
,气象部门预测下个月的平均气温约为6℃,据此估计,该商场下月毛衣的销售量约为 件。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 的样本,问样本中看与不看营养说明的女生各有多少名?
的样本,问样本中看与不看营养说明的女生各有多少名?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.80;8 | B.80;64 | C.70;4 | D.70;3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
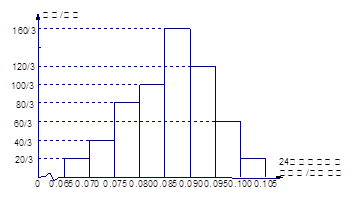
| A.2 | B.3 | C.28 | D.27 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

 =-0.7x+a,则a等于( )
=-0.7x+a,则a等于( )| A.10.5 | B.5.15 | C.5.2 | D.5.25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com