
����Ŀ��Ϊ�˽ⴺ����ҹ�²��С��ij���ӷ�ѿ����֮��Ĺ�ϵ,���ڴ�4�·ݵ�30���������ѡ��5������о�,�ҷֱ��¼��ÿ����ҹ�²���ÿ100�����ӽ��ݺ�ķ�ѿ��,�õ����±���:
���� | 4��1�� | 4��7�� | 4��15�� | 4��21�� | 4��30�� |
�²�x/oC | 10 | 11 | 13 | 12 | 8 |
��ѿ��y/�� | 23 | 25 | 30 | 26 | 16 |
(1)����5������ѡ2��,��ѡȡ����4��1����4��30�յ���������,�������5���е���3�������,���![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]()
(2)�������Իع鷽�̵õ��Ĺ�����������ѡ��������������ݵ�����������2��,����Ϊ�õ������Իع鷽���ǿɿ���,����(1)�����õ����Իع鷽���Ƿ�ɿ�.
(�ο���ʽ, )
)
���𰸡���1��![]() ����2��������.
����2��������.
��������
�����������1�����ݱ��������ݼ�ƽ������ʽ�����![]() ��
��![]() ��ֵ,�Ӷ��ɵ��������ĵ�����꣬������ɵù�ʽ
��ֵ,�Ӷ��ɵ��������ĵ�����꣬������ɵù�ʽ![]()
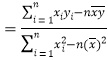 ���������ݣ����
���������ݣ����![]() ���ٽ���������ĵ�����ʿɵ�
���ٽ���������ĵ�����ʿɵ�![]() ���ɵ�
���ɵ�![]() ����
����![]() �Ļع鷽������2����
�Ļع鷽������2����![]() �ֱ��������õĻع鷽�̣����õ���
�ֱ��������õĻع鷽�̣����õ���![]() ֵ��ʵ��ֵ���бȽ�,������Ƿ�
ֵ��ʵ��ֵ���бȽ�,������Ƿ�![]() ���Ӷ��ɵ�(1)�����õ����Իع鷽���Ƿ�ɿ�.
���Ӷ��ɵ�(1)�����õ����Իع鷽���Ƿ�ɿ�.
���������(1)����֪�б����, 4��7��, 4��15��, 4��21����3������ݵ�ƽ����Ϊ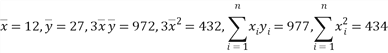 ,����
,����![]() ,����y����x�����Իع鷽��Ϊ
,����y����x�����Իع鷽��Ϊ![]() ,
,
(2)�������,��![]() ʱ,
ʱ,![]() ;��
;��![]() ʱ,
ʱ,![]() ,����(2)�����õ����Իع鷽���ǿɿ���.
,����(2)�����õ����Իع鷽���ǿɿ���.
���������硿������Ҫ�������Իع鷽������Ӧ�ã������е���.��ع�ֱ�߷��̵IJ��裺�������������ݻ���ɢ��ͼ��ȷ��������������������ع�ϵ���ڼ���![]() ��ֵ���ۼ���ع�ϵ��
��ֵ���ۼ���ع�ϵ��![]() ����д���ع�ֱ�߷���Ϊ
����д���ع�ֱ�߷���Ϊ![]() �� �ع�ֱ�߹�����������
�� �ع�ֱ�߹�����������![]() ��һ����Ҫ���ʣ��������Իع鷽�̿��Թ������壬�������Ƿ������������ı仯����.
��һ����Ҫ���ʣ��������Իع鷽�̿��Թ������壬�������Ƿ������������ı仯����.


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
�У�![]() ƽ��
ƽ��![]() ���ı���
���ı���![]() ��ֱ�����Σ�
��ֱ�����Σ�![]() .
.

��1��������![]() ������ֵ��
������ֵ��
��2����![]() ����
����![]() ��һ�㣬
��һ�㣬![]() ��
��![]() ���е㣬��
���е㣬��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵΪ
���ɽǵ�����ֵΪ![]() �����߶�
�����߶�![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������A-BCD�У�AD![]() ƽ��BCD,BC
ƽ��BCD,BC![]() CD,CD=2,AD=4.M��AD���е㣬P��BM���е㣬��Q���߶�AC�ϣ���AQ=3QC.
CD,CD=2,AD=4.M��AD���е㣬P��BM���е㣬��Q���߶�AC�ϣ���AQ=3QC.
(I)֤����PQ//ƽ��BCD;
(II)������ֱ��PQ��CD���ɵĽ�Ϊ![]() �������C-BM-D�Ĵ�СΪ
�������C-BM-D�Ĵ�СΪ![]() ����cos
����cos![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ʱ��̽������
ʱ��̽������![]() �ĵ�������
�ĵ�������
��2��������![]() �IJ���ʽ
�IJ���ʽ![]() ��
��![]() �Ϻ��������
�Ϻ��������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��A1B1C1D1�У�AA1=AB=1��AD=2��EΪBC���е㣬��M��N�ֱ�Ϊ��DD1 �� A1D1���е㣮
��1����֤��ƽ��CMN��ƽ��A1DE��
��2����֤��ƽ��A1DE��ƽ��A1AE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x���Ƕ�����[��2��2]�ϵ��溯������x�ʣ�0��2]ʱ��f��x��=2x��1������g��x��=x2��2x+m���������x1��[��2��2]��x2��[��2��2]��ʹ��g��x2��=f��x1������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ȫ��U=R������A={x|4x��92x+8��0}��B={x| ![]() }��C={x||x��2|��4}����A��B��CUA��C��
}��C={x||x��2|��4}����A��B��CUA��C��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ڣ�0�� ![]() ���ϵĺ���f��x����f'��x��Ϊ�䵼������
���ϵĺ���f��x����f'��x��Ϊ�䵼������ ![]() ��
�� ![]() ��������� ��
��������� ��
A.![]() f��
f�� ![]() ����
���� ![]() f��
f�� ![]() ��
��
B.![]() f��
f�� ![]() ����f��
����f�� ![]() ��??
��??
C.f��1����2f�� ![]() ��sin1
��sin1
D.![]() f��
f�� ![]() ����f��
����f�� ![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com