练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．设a，b∈R，则“$\frac{{a}^{2}}{a-b}$＜0”是“a＜b”的（　　）条件．
    A．充分而不必要B．必要而不充分
    C．充要D．既不充分也不必要

    分析 根据不等式的关系，结合充分条件和必要条件的定义进行求解即可．

    解答 解：由$\frac{{a}^{2}}{a-b}$＜0得a≠0且$\frac{1}{a-b}$＜0，即a≠0且a-b＜0，
    则a≠0且a＜b，则a＜b成立，即充分性成立，
    反之不成立，
    则“$\frac{{a}^{2}}{a-b}$＜0”是“a＜b”的充分不必要条件，
    故选：A．

    点评 本题主要考查充分条件和必要条件的判断，根据不等式的关系进行转化是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．以下关于向量说法的四个选项中正确的选项是（　　）
    A．若任意向量$\overrightarrow a与\overrightarrow b$共线且$\overrightarrow a$为非零向量，则有唯一一个实数λ，使得$\overrightarrow a=λ\overrightarrow b$
    B．对于任意非零向量$\overrightarrow a与\overrightarrow b$，若$（\overrightarrow a+\overrightarrow b）•（\overrightarrow a-\overrightarrow b）=0$，则$|{\overrightarrow a}|=|{\overrightarrow b}|$
    C．任意非零向量$\overrightarrow a与\overrightarrow b$满足$|{\overrightarrow a•\overrightarrow b}|=|{\overrightarrow a}||{\overrightarrow b}|$，则$\overrightarrow a与\overrightarrow b$同向
    D．若A，B，C三点满足$\overrightarrow{OA}=\frac{2}{3}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$，则点A是线段BC的三等分点且离C点较近

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．《九章算术》中有如下问题：“今有勾八步，股一十五步，问勾中容圆，径几何？”其大意：“已知直角三角形两直角边长分别为8步和15步，问其内切圆的直径为多少步？”现若向此三角形内随机投一粒豆子，则豆子落在其内切圆外的概率是（　　）
    A．$\frac{3π}{10}$B．$\frac{3π}{20}$C．$1-\frac{3π}{10}$D．$1-\frac{3π}{20}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．若数列{an}满足a1=1，log2an+1=log2an+1（n∈N*），它的前n项和为Sn，则Sn=（　　）
    A．2-21-nB．2n-1-1C．2n-1D．2-2n-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．在下列条件中，可以判断三角形有两解的是（　　）
    A．A=30°．B=45°．c=10B．a=$\sqrt{3}$．c=$\sqrt{2}$．B=45°
    C．a=14．c=16．A=45°D．c=7．b=5．C=80°

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．要得到函数y=$\frac{\sqrt{3}}{2}$sin2x+cos2x-$\frac{1}{2}$的图象，只需将y=sinx图象上所有的点（　　）
    A．横坐标变为原来的一半，纵坐标不变，再向左平移$\frac{π}{6}$个单位
    B．横坐标变为原来的两倍，纵坐标不变，再向左平移$\frac{π}{12}$个单位
    C．向左平移$\frac{π}{12}$个单位，再将所得各点的横坐标变为原来的两倍，纵坐标不变
    D．向左平移$\frac{π}{6}$个单位，再将所得各点的横坐标变为原来的一半，纵坐标不变

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．以圆形摩天轮的轴心O为原点，水平方向为x轴，在摩天轮所在的平面建立直角坐标系，设摩天轮的半径为20米，把摩天轮上的一个吊篮看作一个点P0，起始时点P0在-$\frac{π}{6}$的终边上，OP0绕O按逆时针方向作匀速旋转运动，其角速度为$\frac{π}{5}$（弧度/分），经过t分钟后，OP0到达OP，记P点的横坐标为m，则m关于时间t的函数图象为 （　　）
    A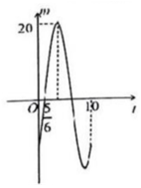．B．C．D．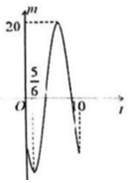

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．圆x2+y2-6x+4y=3的圆心坐标与半径是（　　）
    A．$（-3，2）\;\;\;\;\;\;\;\sqrt{13}$B．$（3，-2）\;\;\;\;\;\;\;\sqrt{13}$C．（-3，2）4D．（3，-2）4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知sin（$\frac{π}{3}$+α）=$\frac{3}{5}$，$\frac{π}{6}$＜α＜$\frac{2π}{3}$，则cosα=$\frac{3\sqrt{3}-4}{10}$．

    查看答案和解析>>

    同步练习册答案