
分析 (Ⅰ)利用动点P(x,y)到定点F(1,0)的距离与它到定直线l:x=4的距离之比为$\frac{1}{2}$,列出方程化简并整理,即可得到动点P(x,y)的轨迹C的方程.
(Ⅱ)当t=0时,说明M,N,F三点共线,当t≠0时得到$QA:y=\frac{t}{6}(x+2),QB:y=\frac{t}{2}(x-2)$,分别与椭圆联立方程组求解M、N的横坐标,通过共线的充要条件,证明即可.
解答 (本小题共14分)
解:(Ⅰ)由题意动点P(x,y)到定点F(1,0)的距离与它到定直线l:x=4的距离之比为$\frac{1}{2}$,
得$\frac{{\sqrt{{{(x-1)}^2}+{y^2}}}}{|x-4|}=\frac{1}{2}$,…(2分)
化简并整理,得 $\frac{x^2}{4}+\frac{y^2}{3}=1$.
所以动点P(x,y)的轨迹C的方程为椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$.…(5分)
(Ⅱ)当t=0时,点M与B重合,点N与A重合,M,N,F三点共线.…(7分)
当t≠0时
根据题意:$QA:y=\frac{t}{6}(x+2),QB:y=\frac{t}{2}(x-2)$
由$\left\{\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{3}=1\\ y=\frac{t}{6}({x+2})\end{array}\right.$
消元得:$3{x^2}+\frac{t^2}{9}{(x+2)^2}-12=0$
整理得:(t2+27)x2+4t2x+4t2-108=0
该方程有一根为x=-2,另一根为xM,根据韦达定理,$-2{x_M}=\frac{{4{t^2}-108}}{{{t^2}+27}},{x_M}=\frac{{54-2{t^2}}}{{{t^2}+27}}$
由$\left\{\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{3}=1\\ y=\frac{t}{2}({x-2})\end{array}\right.$
消元得:3x2+t2(x-2)2-12=0
整理得:(t2+3)x2-4t2x+4t2-12=0
该方程有一根为x=2,另一根为xN,根据韦达定理,$2{x_N}=\frac{{4{t^2}-12}}{{{t^2}+3}},{x_N}=\frac{{2{t^2}-6}}{{{t^2}+3}}$
当xM=xN时,由$\frac{{54-2{t^2}}}{{{t^2}+27}}=\frac{{2{t^2}-6}}{{{t^2}+3}}$
得:t2=9,xM=xN=1,M,N,F三点共线;
当xM≠xN时,${y_M}=\frac{t}{6}({x_M}+2)=\frac{18t}{{{t^2}+27}}$,${y_N}=\frac{t}{2}({x_N}-2)=\frac{-6t}{{{t^2}+3}}$${k_{MF}}=\frac{y_M}{{{x_M}-1}}=\frac{{\frac{18t}{{{t^2}+27}}}}{{\frac{{54-2{t^2}}}{{{t^2}+27}}-1}}=\frac{6t}{{9-{t^2}}}$;${k_{NF}}=\frac{y_N}{{{x_N}-1}}=\frac{{\frac{-6t}{{{t^2}+3}}}}{{\frac{{2{t^2}-6}}{{{t^2}+3}}-1}}=\frac{6t}{{9-{t^2}}}$kMF=KNF,M,N,F三点共线.
综上,命题恒成立.…(14分)
点评 本题考查轨迹方程的求法,直线与椭圆的位置关系的综合应用,三点共线的充要条件的应用,考查分析问题解决问题的能力,转化思想的应用.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 48 | C. | 72 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
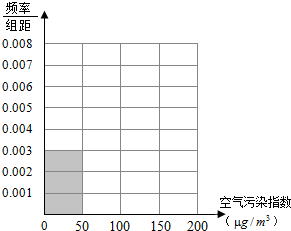 空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2015年1月某日某省x个监测点数据统计如下:
空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2015年1月某日某省x个监测点数据统计如下:| 空气污染指数 (单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 已知两个命题p,q,若p∧q为假命题,则p∨q也为假命题 | |
| B. | 实数a=0是直线ax-2y=1与2ax-2y=3平行的充要条件 | |
| C. | “?x0∈R,使得x02+2x0+5=0“的否定是“?x∈R,都有x2+2x+5≠0“ | |
| D. | 命题p:?x∈R,x2+1≥1;命题q:?x∈R,x2-x+1≤0,则命题p∧(¬q)是真命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com