
分析 (Ⅰ)根据二倍角的正余弦公式,和两角和的正弦公式即可化简f(x)=$2sin(x+\frac{π}{6})$,而由x的范围可以求出x+$\frac{π}{6}$的范围,从而可得出f(x)的值域;
(Ⅱ)由f(A)=2即可求得A=$\frac{π}{3}$,从而由余弦定理和不等式a2+b2≥2ab可求得|AB||AC|≤1,根据向量数量积的计算公式便可得出$\overrightarrow{AB}•\overrightarrow{AC}$的最大值.
解答 解:(Ⅰ)$f(x)=\sqrt{3}sinx+cosx=2sin(x+\frac{π}{6})$;
∵$x∈[\frac{π}{6},\frac{2π}{3}]$;
∴$x+\frac{π}{6}∈[\frac{π}{3},\frac{5π}{6}]$;
∴$\frac{1}{2}≤sin(x+\frac{π}{6})≤1$;
∴f(x)的值域为[1,2];
(Ⅱ)∵f(A)=2,∴$sin(A+\frac{π}{6})=1$;
在△ABC中,∵0<A<π,∴$A=\frac{π}{3}$;
∴$cosA=\frac{{{{|{AB}|}^2}+{{|{AC}|}^2}-{{|{BC}|}^2}}}{{2|{AB}||{AC}|}}=\frac{1}{2}$;
∴|AB||AC|=|AB|2+|AC|2-1≥2|AB||AC|-1;
∴|AB||AC|≤1;
∴$\overrightarrow{AB}•\overrightarrow{AC}=|{AB}||{AC}|cosA=\frac{1}{2}|{AB}||{AC}|≤\frac{1}{2}$;
∴$\overrightarrow{AB}•\overrightarrow{AC}$的最大值为$\frac{1}{2}$.
点评 考查二倍角的正余弦公式,两角和的正弦公式,以及余弦定理,已知三角函数值求角,不等式a2+b2≥2ab的运用,数量积的计算公式.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
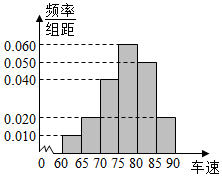 2016年“双节”期间,高速公路车辆较多,某调查公司在一服务区从小型汽车中按进服务区的先后每间隔35辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:
2016年“双节”期间,高速公路车辆较多,某调查公司在一服务区从小型汽车中按进服务区的先后每间隔35辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-17)<f(19)<f(40) | B. | f(40)<f(19)<f(-17) | C. | f(19)<f(40)<f(-17) | D. | f(-17)<f(40)<f(19) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com