
分析 利用等比数列的通项公式、等差数列的求和公式、指数运算法则可知${{a}_{1}}^{30}$=4-15×27,通过数列{a3n-2}是公比为43的等比数列,计算可知所求值为${{a}_{1}}^{10}$•415×27,利用${{a}_{1}}^{10}$=$\root{3}{{{a}_{1}}^{30}}$代入计算即得结论.
解答 解:依题意,a1•a2•a3…•a30=${{a}_{1}}^{30}$•q0+1+2+…+29
=${{a}_{1}}^{30}$•${4}^{\frac{30×(0+29)}{2}}$
=${{a}_{1}}^{30}$•415×29
=430,
∴${{a}_{1}}^{30}$=430-15×29=4-15×27,
又∵数列{a3n-2}是公比为43的等比数列,
∴a1•a4•a7…a28=${{a}_{1}}^{10}$•q0+3+6+…+27
=${{a}_{1}}^{10}$•${4}^{3•\frac{10×(0+27)}{2}}$
=${{a}_{1}}^{10}$•415×27,
又∵${{a}_{1}}^{10}$=$\root{3}{{{a}_{1}}^{30}}$=${4}^{\frac{-15×27}{3}}$=4-5×27,
∴${{a}_{1}}^{10}$•415×27=4-5×27•415×27=4270,
即a1•a4•a7…a28=4270,
故答案为:4270.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:填空题
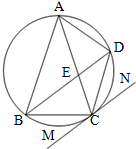 如图,四边形ABCD内接于圆,AB=AC,直线MN切圆于点C,BD∥MN交AC于点E.若AB=6,BC=4,则AE的长为$\frac{10}{3}$.
如图,四边形ABCD内接于圆,AB=AC,直线MN切圆于点C,BD∥MN交AC于点E.若AB=6,BC=4,则AE的长为$\frac{10}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com