
【题目】已知等比数列{an}的公比q≠1,则下面说法中不正确的是( )
A.{an+2+an}是等比数列
B.对于k∈N* , k>1,ak﹣1+ak+1≠2ak
C.对于n∈N* , 都有anan+2>0
D.若a2>a1 , 则对于任意n∈N* , 都有an+1>an
科目:高中数学 来源: 题型:
【题目】(本小题满分为16分)为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,新上了把二氧化碳处理转化为一种可利用的化工产品的项目,经测算,该项目月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为:
 ,且每处理一吨二氧化碳得到可利用的化工产品价值为200元,若该项目不获利,国家将给予补偿.
,且每处理一吨二氧化碳得到可利用的化工产品价值为200元,若该项目不获利,国家将给予补偿.
(1)当x∈[200,300]时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则国家每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题
(1)在边长为1的正方形ABCD内任取一点M,求事件“|AM|≤1”的概率;
(2)某班在一次数学活动中,老师让全班56名同学每人随机写下一对都小于1的正实数x、y,统计出两数能与1构成锐角三角形的三边长的数对(x,y)共有12对,请据此估计π的近似值(精确到0.001).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|.
(1)若f(x)≤m的解集为{x|﹣1≤x≤5},求实数a,m的值.
(2)当a=2且0≤t<2时,解关于x的不等式f(x)+t≥f(x+2).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分为16分)已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的极值,并指出极大值还是极小值;
的极值,并指出极大值还是极小值;
(2)若![]() ,求函数
,求函数![]() 在
在![]() 上的最值;
上的最值;
(3)若![]() ,求证:在区间
,求证:在区间![]() 上,函数
上,函数![]() 的图象在
的图象在![]() 的图象下方.
的图象下方.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线 ![]() ﹣
﹣ ![]() =1与直线y=2x+m有两个交点,则m的取值范围是( )
=1与直线y=2x+m有两个交点,则m的取值范围是( )
A.(﹣∞,﹣4)∪(4,+∞)
B.(﹣4,4)
C.(﹣∞,﹣3)∪(3,+∞)
D.(﹣3,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视传媒公司为了了解某类体育节目的收视情况,随机抽取了100名观众进行调查,如图是根据调查结果绘制的观众日均收看该类体育节目时间的频率分布直方图,其中收看时间分组区间是:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60].将日均收看该类体育节目时间不低于40分钟的观众称为“体育迷”.则抽取的100名观众中“体育迷”有名. 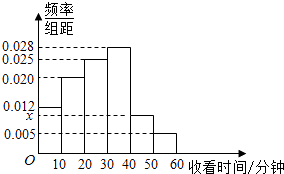
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)已知函数![]() ,
, ![]() .
.
(1)若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若直线![]() 是函数
是函数![]() 图象的切线,求
图象的切线,求![]() 的最小值;
的最小值;
(3)当![]() 时,若
时,若![]() 与
与![]() 的图象有两个交点
的图象有两个交点![]() ,求证:
,求证: ![]()
![]() .(取
.(取![]() 为
为![]() ,取
,取![]() 为
为![]() ,取
,取![]() 为
为![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com