
分析 根据题意,设A(x1,y1),B(x2,y2),P(x0,y0),由圆的切线方程可得PA、PB的方程,而PA、PB交于P(x0,y0),由此能求出AB的直线方程,从而可得三角形的面积,利用基本不等式可求最值.
解答 解:根据题意,设A(x1,y1),B(x2,y2),P(x0,y0),
PA是圆的切线且切点为A,则PA的方程为x1x+y1y=4,
同理PB的方程为x2x+y2y=4,
又由PA、PB交与点P,则有x1x0+y1y0=4,x2x0+y2y0=4,
则直线AB的方程为x0x+y0y=4,
则M的坐标为($\frac{4}{{x}_{0}}$,0),N的坐标为(0,$\frac{4}{{y}_{0}}$),
S△OMN=$\frac{1}{2}$|OM||ON|=$\frac{8}{|{x}_{0}{y}_{0}|}$,
又由点P是椭圆$\frac{x^2}{8}+\frac{y^2}{4}=1$在第一象限上的动点,则有$\frac{{{x}_{0}}^{2}}{8}$+$\frac{{{y}_{0}}^{2}}{4}$=1,
则有1=$\frac{{{x}_{0}}^{2}}{8}$+$\frac{{{y}_{0}}^{2}}{4}$≥2$\sqrt{\frac{{{x}_{0}}^{2}}{8}×\frac{{{y}_{0}}^{2}}{4}}$=$\frac{\sqrt{2}}{8}$|x0y0|,即|x0y0|≤4$\sqrt{2}$,
S△OMN=$\frac{1}{2}$|OM||ON||=$\frac{8}{|{x}_{0}{y}_{0}|}$≥$\sqrt{2}$,
即△OMN面积的最小值为$\sqrt{2}$;
故答案为:$\sqrt{2}$.
点评 本题考查椭圆的几何性质,涉及直线与圆的切线方程,关键是由圆的切线方程分析得到直线AB的方程.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥-2} | B. | {x|x>-2} | C. | {x|1<x<3} | D. | {x|1<x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -i | B. | i | C. | $\frac{4}{5}-i$ | D. | $\frac{4}{5}-\frac{3}{5}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
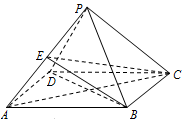 已知四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,$PA=\sqrt{6}$.
已知四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,$PA=\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2) | B. | [0,2] | C. | [-2,0] | D. | [-2,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 30 | C. | 40 | D. | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
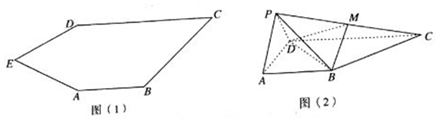
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
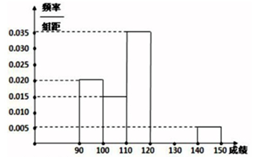
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com