练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．某工厂生产A、B、C三种不同型号的产品，某月生产产品数量之比依次为m：3：2，现用分层抽样方法抽取一个容量为120的样本，已知A种型号产品抽取了45件，则C种型号产品抽取的件数为（　　）
    A．20B．30C．40D．45

    分析 先求出B、C两种型号的产品共抽取：120-45=75，由此利用分层抽栏的性质能求出C种型号产品抽取的件数．

    解答 解：∵分层抽样方法抽取一个容量为120的样本，A种型号产品抽取了45件，
    ∴B、C两种型号的产品共抽取：120-45=75，
    ∵某工厂生产A、B、C三种不同型号的产品，某月生产产品数量之比依次为m：3：2，
    ∴C种型号产品抽取的件数为：75×$\frac{2}{3+2}$=30．
    故选：B．

    点评 本题考查分层抽样的应用，是基础题，解题时要认真审题，注意分层抽样性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    17．若随机变量ξ服从正态分布N（μ，σ2），P（μ-σ＜ξ＜μ+σ）=0.6826，P（μ-2σ＜ξ＜μ+2σ）=0.9544，设ξ～N（1，σ2），且P（ξ≥3）=0.1587，在平面直角坐标系xOy中，若圆x2+y2=σ2上有四个点到直线12x-5y+c=0的距离为1，则实数c的取值范围是（-13，13）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数$f（x）=\frac{{{x^2}-1}}{{lnx-a{x^2}}}（a∈$R）．
    （1）当a=0时，求函数 f（x）的单调区间；
    （2）若对于任意x∈（1，e），不等式f（x）＞1恒成立，求 a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知点P是椭圆$\frac{x^2}{8}+\frac{y^2}{4}=1$在第一象限上的动点，过点P引圆x2+y2=4的两条切线PA、PB，切点分别是A、B，直线AB与x轴、y轴分别交于点M、N，则△OMN面积的最小值为$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

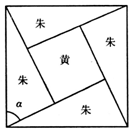    2．三国时代吴国数学家赵爽所著《周髀算经》中用赵爽弦图给出了勾股定理的绝妙证明，如图是赵爽弦图，图中包含四个全等的勾股形及一个小正方形，分别涂成朱色和黄色，若朱色的勾股形中较大的锐角α为$\frac{π}{3}$，现向该赵爽弦图中随机地投掷一枚飞镖，则飞镖落在黄色的小正方形内的概率为1-$\frac{\sqrt{3}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．若函数$f（x）=\left\{\begin{array}{l}{x^2}+\frac{2}{x}，x＞0\\ a{x^2}+\frac{b}{x}，x＜0\end{array}\right.$是奇函数，则f（a-b）=-$\frac{29}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．如果x，y满足$\left\{\begin{array}{l}{x-2y-4≤0}\\{x+y-1≥0}\\{2x-y-2≥0}\end{array}\right.$，则z=$\frac{y+1}{x+1}$的取值范围是（　　）
    A．[0，2）B．[0，2]C．[-1，$\frac{1}{2}$]D．[0，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．某农科所发现，一中作物的年收获量y（单位：kg）与它”相近“作物的株数x具有线性相关关系（所谓两株作物”相近“是指它们的直线距离不超过1m），并分别记录了相近作物的株数为1，2，3，5，6，7时，该作物的年收获量的相关数据如下：
    X123567
    y605553464541
    （Ⅰ）求该作物的年收获量y关于它”相近“作物的株数x的线性回归方程；
    （Ⅱ）农科所在如图所示的正方形地块的每个格点（指纵、横直线的交叉点）处都种了一株该作物，其中每一个小正方形的面积为1，若在所种作物中随机选取一株，求它的年收获量的分布列与数学期望．（注：年收获量以线性回归方程计算所得数据为依据）
    附：对于一组数据（x1，y1），（x2，y2），…，（xn，yn），其回归直线y=a+bx的斜率和截距的最小二乘估计分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n•{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．直线l：x+λy+2-3λ=0（λ∈R）恒过定点（-2，3），P（1，1）到该直线的距离最大值为$\sqrt{13}$．

    查看答案和解析>>

    同步练习册答案