
分析 根据正态分布特点计算P(-1<ξ<3)=0.6826,从而得出σ=2,根据直线与圆的位置关系得出圆心到直线的距离范围,从而得出c的范围.
解答 解:$P(ξ≥3)=P(ξ≤-1)=\frac{1}{2}[1-P(-1<ξ<3)]⇒P(-1<ξ<3)=0.6826$,
∴1-σ=-1,1+σ=3,故σ=2,
∴圆的半径为2,
∵圆上有四个点到直线12x-5y+c=0的距离为1,
∴圆心(0,0)到直线的距离d满足0≤d<1.
∵$d=\frac{|c|}{{\sqrt{{{12}^2}+{5^2}}}}=\frac{|c|}{13}$,
∴0≤|c|<13,即c∈(-13,13).
故答案为(-13,13).
点评 本题考查了正态分布的特点,直线与圆的位置关系,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8π | B. | 12π | C. | 20π | D. | 24π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
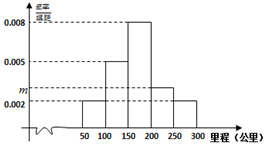 绿色出行越来越受到社会的关注,越来越多的消费者对新能源汽车感兴趣.但是消费者比较关心的问题是汽车的续驶里程.某研究小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.
绿色出行越来越受到社会的关注,越来越多的消费者对新能源汽车感兴趣.但是消费者比较关心的问题是汽车的续驶里程.某研究小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥-2} | B. | {x|x>-2} | C. | {x|1<x<3} | D. | {x|1<x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 30 | C. | 40 | D. | 45 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com