
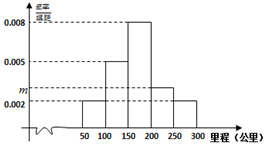
 绿色出行越来越受到社会的关注,越来越多的消费者对新能源汽车感兴趣.但是消费者比较关心的问题是汽车的续驶里程.某研究小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.
绿色出行越来越受到社会的关注,越来越多的消费者对新能源汽车感兴趣.但是消费者比较关心的问题是汽车的续驶里程.某研究小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.分析 (1)利用小矩形的面积和为1,求得m值;
(2)求得续驶里程在[200,300]的车辆的频率,再利用频数=频率×样本容量求车辆数;
(3)利用排列组合,分别求得5辆中随机抽取2辆车的抽法种数与其中恰有一辆汽车的续驶里程为[200,250)抽法种数,根据古典概型的概率公式计算.
解答 解:(1)有直方图可得:(0.002+0.005+0.008+m+0.002)×50=1得m=0.003…(3分)
(2)由题意知续驶里程在[200,300]的车辆数为20×(0.003×50+0.002×50)=5…(6分)
(3)由题意知,续驶里程在[200,250)的车辆数为3,设为a,b,c,
续驶里程在[250,300]的车辆数为2,设为d,e,
共有10个基本事件:ab,ac,ad,ae,bc,bd,be,cd,ce,de,
设“其中恰有一辆车续驶里程在[200,250]”为事件A,
则事件A包含6个基本事件:ad,ae,bc,bd,be,cd,ce,
则$P(A)=\frac{6}{10}=\frac{3}{5}$…(12分)
点评 本题考查了频率分布直方图,古典概型的概率计算,在频率分布直方图中频率=小矩形的面积=小矩形的高×组距=$\frac{频数}{样本容量}$.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f'(m)<0,f'(n)<0 | B. | f'(m)>0,f'(n)>0 | C. | f'(m)<0,f'(n)>0 | D. | f'(m)>0,f'(n)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2<x<1} | B. | {x|x<-2} | C. | {x|x<1} | D. | {x|x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2) | B. | [0,2] | C. | [-1,$\frac{1}{2}$] | D. | [0,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com