
分析 (1)运用因式分解,可得(an+1-an-1)2=0,再由等差数列的通项公式,即可得到所求;
(2)由$\frac{1}{{{a}_{n}}^{2}}$=$\frac{1}{{n}^{2}}$<$\frac{1}{n(n-1)}$=$\frac{1}{n-1}$-$\frac{1}{n}$,n≥2.对原不等式左边从第三项开始放大,再由不等式的性质,即可得证;
(3)运用数学归纳法证明,首先验证n=2成立,假设n=k≥2,都有Sk2>2($\frac{{S}_{2}}{2}$+$\frac{{S}_{3}}{3}$+…+$\frac{{S}_{k}}{k}$).再证n=k+1,注意运用假设和不等式的性质,即可得证.
解答 解:(1)a1=1,且an+12+an2=2(an+1an+an+1-an-$\frac{1}{2}$),
可得an+12+an2-2an+1an-2an+1+2an+1=0,
即有(an+1-an)2-2(an+1-an)+1=0,
即为(an+1-an-1)2=0,
可得an+1-an=1,
则an=a1+n-1=n,n∈N*;
(2)证明:由$\frac{1}{{{a}_{n}}^{2}}$=$\frac{1}{{n}^{2}}$<$\frac{1}{n(n-1)}$=$\frac{1}{n-1}$-$\frac{1}{n}$,n≥2.
则$\frac{1}{{{a}_{1}}^{2}}$+$\frac{1}{{{a}_{2}}^{2}}$+…+$\frac{1}{{{a}_{n}}^{2}}$=1+$\frac{1}{4}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$
<1+$\frac{1}{4}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n-1}$-$\frac{1}{n}$=$\frac{7}{4}$-$\frac{1}{n}$<$\frac{7}{4}$,
故原不等式成立;
(3)证明:Sn=$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$=1+$\frac{1}{2}$+…+$\frac{1}{n}$,
当n=2时,S22=(1+$\frac{1}{2}$)2=$\frac{9}{4}$>2•$\frac{{S}_{2}}{2}$=$\frac{3}{2}$成立;
假设n=k≥2,都有Sk2>2($\frac{{S}_{2}}{2}$+$\frac{{S}_{3}}{3}$+…+$\frac{{S}_{k}}{k}$).
则n=k+1时,Sk+12=(Sk+$\frac{1}{k+1}$)2,
Sk+12-2($\frac{{S}_{2}}{2}$+$\frac{{S}_{3}}{3}$+…+$\frac{{S}_{k}}{k}$+$\frac{{S}_{k+1}}{k+1}$)
=(Sk+$\frac{1}{k+1}$)2-2($\frac{{S}_{2}}{2}$+$\frac{{S}_{3}}{3}$+…+$\frac{{S}_{k}}{k}$)-2•$\frac{{S}_{k+1}}{k+1}$
=Sk2-2($\frac{{S}_{2}}{2}$+$\frac{{S}_{3}}{3}$+…+$\frac{{S}_{k}}{k}$)+$\frac{1}{(k+1)^{2}}$+2•$\frac{{S}_{k}}{k+1}$-2•$\frac{{S}_{k+1}}{k+1}$
=Sk2-2($\frac{{S}_{2}}{2}$+$\frac{{S}_{3}}{3}$+…+$\frac{{S}_{k}}{k}$)+$\frac{k-1}{(k+1)^{2}}$,
由k>1可得$\frac{k-1}{(k+1)^{2}}$>0,
且Sk2>2($\frac{{S}_{2}}{2}$+$\frac{{S}_{3}}{3}$+…+$\frac{{S}_{k}}{k}$).
可得Sk2-2($\frac{{S}_{2}}{2}$+$\frac{{S}_{3}}{3}$+…+$\frac{{S}_{k}}{k}$)>0,
则Sk+12>2($\frac{{S}_{2}}{2}$+$\frac{{S}_{3}}{3}$+…+$\frac{{S}_{k}}{k}$+$\frac{{S}_{k+1}}{k+1}$)恒成立.
综上可得,对于一切n≥2,都有Sn2>2($\frac{{S}_{2}}{2}$+$\frac{{S}_{3}}{3}$+…+$\frac{{S}_{n}}{n}$).
点评 本题考查数列的通项公式的求法,注意运用因式分解和等差数列的定义和通项公式,考查数列不等式的证明,注意运用放缩法和数学归纳法,考查推理和运算能力,属于难题.


科目:高中数学 来源: 题型:解答题
| 学生编号 | A1 | A2 | A3 | A4 | A5 |
| 评价指数(x,y,z) | (3,4,3) | (4,3,4) | (4,4,2) | (4,3,5) | (4,5,4) |
| 学生编号 | B1 | B2 | B3 | B4 | B5 |
| 评价指数(x,y,z) | (3,5,3) | (4,3,2) | (5,4,4) | (5,4,5) | (4,5,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
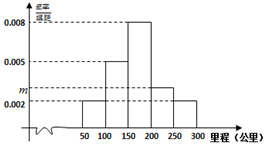 绿色出行越来越受到社会的关注,越来越多的消费者对新能源汽车感兴趣.但是消费者比较关心的问题是汽车的续驶里程.某研究小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.
绿色出行越来越受到社会的关注,越来越多的消费者对新能源汽车感兴趣.但是消费者比较关心的问题是汽车的续驶里程.某研究小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
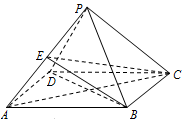 已知四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,$PA=\sqrt{6}$.
已知四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,$PA=\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com