
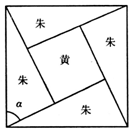
 三国时代吴国数学家赵爽所著《周髀算经》中用赵爽弦图给出了勾股定理的绝妙证明,如图是赵爽弦图,图中包含四个全等的勾股形及一个小正方形,分别涂成朱色和黄色,若朱色的勾股形中较大的锐角α为$\frac{π}{3}$,现向该赵爽弦图中随机地投掷一枚飞镖,则飞镖落在黄色的小正方形内的概率为1-$\frac{\sqrt{3}}{2}$.
三国时代吴国数学家赵爽所著《周髀算经》中用赵爽弦图给出了勾股定理的绝妙证明,如图是赵爽弦图,图中包含四个全等的勾股形及一个小正方形,分别涂成朱色和黄色,若朱色的勾股形中较大的锐角α为$\frac{π}{3}$,现向该赵爽弦图中随机地投掷一枚飞镖,则飞镖落在黄色的小正方形内的概率为1-$\frac{\sqrt{3}}{2}$.  全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:解答题
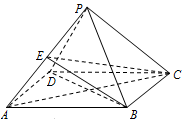 已知四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,$PA=\sqrt{6}$.
已知四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,$PA=\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
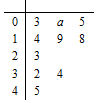 已知函数f(x)=x2+$\sqrt{2}(m-1)x+\frac{m}{4}$,现有一组数据,绘制得到茎叶图,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)
已知函数f(x)=x2+$\sqrt{2}(m-1)x+\frac{m}{4}$,现有一组数据,绘制得到茎叶图,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 30 | C. | 40 | D. | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
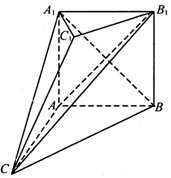 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,A1C=BC,B1C1∥BC,且${B_1}{C_1}=\frac{1}{2}BC$.
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,A1C=BC,B1C1∥BC,且${B_1}{C_1}=\frac{1}{2}BC$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com