
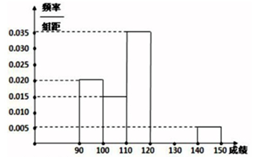
分析 (1)由频率分布直方图得第六组的频率为:0.05,由第六组有2人,求出样本单元数n=40,再由第四、五、六组的人数依次成等差数列,且第六组有2人,求出第四组小矩形的高,第五组小矩形的高,由此能完成频率分布直方图.
(2)该班成绩在[130,140]的学生有4人,成绩在[140,150]的学生有2人,从成绩在[130,150)的学生中任选三人参加省数学竞赛,基本事件总数n=${C}_{6}^{3}$=20,随机变量X表示成绩在[130,140)的人数,则X的可能取值为1,2,3,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(1)由频率分布直方图得:
第六组的频率为:0.005×10=0.05,
∵第六组有2人,∴样本单元数n=$\frac{2}{0.05}$=40,
∵第四、五、六组的人数依次成等差数列,且第六组有2人,
设公差为d,
∴0.020×10×40+0.015×10×40+0.035×10×40+(2+2d)+(2+d)+2=40,
解得d=2,
∴第四组小矩形的高为:$\frac{6}{40}$÷10=0.015,
第五组小矩形的高为:$\frac{4}{40}÷10$=0.010.
∴频率分布直方图为:
(2)该班成绩在[130,140]的学生有4人,成绩在[140,150]的学生有2人,
从成绩在[130,150)的学生中任选三人参加省数学竞赛,
基本事件总数n=${C}_{6}^{3}$=20,
随机变量X表示成绩在[130,140)的人数,则X的可能取值为1,2,3,
P(X=1)=$\frac{{C}_{4}^{1}{C}_{2}^{2}}{{C}_{6}^{3}}$=$\frac{4}{20}$=$\frac{1}{5}$,
P(X=2)=$\frac{{C}_{4}^{2}{C}_{2}^{1}}{{C}_{6}^{3}}$=$\frac{12}{20}$=$\frac{3}{5}$,
P(X=3)=$\frac{{C}_{4}^{3}}{{C}_{6}^{3}}$=$\frac{4}{20}$=$\frac{1}{5}$,
∴X的分布列为:
| X | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查频率分布直方图、离散型随机变量的分布列、数学期望等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某农科所发现,一中作物的年收获量y(单位:kg)与它”相近“作物的株数x具有线性相关关系(所谓两株作物”相近“是指它们的直线距离不超过1m),并分别记录了相近作物的株数为1,2,3,5,6,7时,该作物的年收获量的相关数据如下:
某农科所发现,一中作物的年收获量y(单位:kg)与它”相近“作物的株数x具有线性相关关系(所谓两株作物”相近“是指它们的直线距离不超过1m),并分别记录了相近作物的株数为1,2,3,5,6,7时,该作物的年收获量的相关数据如下:| X | 1 | 2 | 3 | 5 | 6 | 7 |
| y | 60 | 55 | 53 | 46 | 45 | 41 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨q | C. | (¬p)∧(¬q) | D. | p∨(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
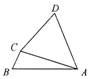 如图,在四边形ABCD中,∠B=$\frac{π}{3}$,∠BCA=2∠CAD,CD=2$\sqrt{2}$,AD=AC=4,则AB=$\sqrt{21}$.
如图,在四边形ABCD中,∠B=$\frac{π}{3}$,∠BCA=2∠CAD,CD=2$\sqrt{2}$,AD=AC=4,则AB=$\sqrt{21}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,5) | B. | (-∞,0) | C. | (3,5] | D. | [3,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com