
| A. | (3,5) | B. | (-∞,0) | C. | (3,5] | D. | [3,+∞) |
分析 由不等式进行转化,然后判断函数的单调性,求函数的导数,利用参数分离法进行求解即可.
解答 解:∵p≠q,不妨设p>q,由于$\frac{f(p)-f(q)}{p-q}>1$,
∴f(p)-f(q)>p-q,得[f(p)-p]-[f(q)-q]>0,
∵p>q,∴g(x)=f(x)-x在(0,1)内是增函数,
∴g'(x)>0在(0,1)内恒成立,即$\frac{a}{x}-2x-1$>0恒成立,
a>x(2x+1)的最大值,
∵x∈(0,1)时x(2x+1)<3,
∴实数a的取值范围为[3,+∞).
故选:D.
点评 本题主要考查不等式恒成立问题,根据不等式进行转化判断函数的单调性,分离参数是解决本题的关键,是中档题.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 216 | B. | 108 | C. | 432 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验次数 |
| A | 甲 | 2次 | 6次 | 4次 | 12次 |
| B | 乙 | 3次 | 6次 | 3次 | 12次 |
| C | 丙 | 2次 | 2次 | 8次 | 12次 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
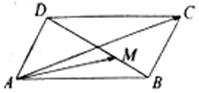 如图,平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,$\overrightarrow{DM}=2\overrightarrow{MB}$,则$\overrightarrow{AC}•\overrightarrow{AM}$=4.
如图,平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,$\overrightarrow{DM}=2\overrightarrow{MB}$,则$\overrightarrow{AC}•\overrightarrow{AM}$=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
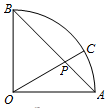 如图,扇形AOB的圆心角为90°,点P在弦AB上,且OP=$\sqrt{2}$AP,延长OP交弧AB于点C,现向该扇形内随机投一点,则该点落在扇形AOC内的概率为$\frac{1}{3}$.
如图,扇形AOB的圆心角为90°,点P在弦AB上,且OP=$\sqrt{2}$AP,延长OP交弧AB于点C,现向该扇形内随机投一点,则该点落在扇形AOC内的概率为$\frac{1}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com