在2016年巴西里约奥运会期间.6名游泳队员从左至右排成一排合影留念.最左边只能排甲或乙.最右端不能排甲.则不同的排法种数为( )A．216B．108C．432D．120 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

6．在2016年巴西里约奥运会期间，6名游泳队员从左至右排成一排合影留念，最左边只能排甲或乙，最右端不能排甲，则不同的排法种数为（　　）

A．

216

B．

108

C．

432

D．

120

分析根据题意，分2种情况讨论：①、最左边排甲，①、最左边排乙，分别求出每一种情况的安排方法数目，由分类计数原理计算可得答案．

解答解：根据题意，最左边只能排甲或乙，则分2种情况讨论：
①、最左边排甲，则先在剩余5个位置选一个安排乙，乙有5种情况，
再将剩余的4个人全排列，安排在其余4个位置，有A₄⁴=24种安排方法，
此时有5×24=120种情况，
①、最左边排乙，由于最右端不能排甲，则甲有4个位置可选，有4种情况，
再将剩余的4个人全排列，安排在其余4个位置，有A₄⁴=24种安排方法，
此时有4×24=96种情况，
则不同的排法种数为120+96=216种；
故选：A．

点评本题考查排列、组合的实际应用，注意要先分析特殊元素，由本题的甲、乙．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

16．

某农科所发现，一中作物的年收获量y（单位：kg）与它”相近“作物的株数x具有线性相关关系（所谓两株作物”相近“是指它们的直线距离不超过1m），并分别记录了相近作物的株数为1，2，3，5，6，7时，该作物的年收获量的相关数据如下：

X	1	2	3	5	6	7
y	60	55	53	46	45	41

（Ⅰ）求该作物的年收获量y关于它”相近“作物的株数x的线性回归方程；
（Ⅱ）农科所在如图所示的正方形地块的每个格点（指纵、横直线的交叉点）处都种了一株该作物，其中每一个小正方形的面积为1，若在所种作物中随机选取一株，求它的年收获量的分布列与数学期望．（注：年收获量以线性回归方程计算所得数据为依据）
附：对于一组数据（x₁，y₁），（x₂，y₂），…，（x_n，y_n），其回归直线y=a+bx的斜率和截距的最小二乘估计分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n•{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

17．直线l：x+λy+2-3λ=0（λ∈R）恒过定点（-2，3），P（1，1）到该直线的距离最大值为$\sqrt{13}$．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

14．

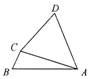如图，在四边形ABCD中，∠B=$\frac{π}{3}$，∠BCA=2∠CAD，CD=2$\sqrt{2}$，AD=AC=4，则AB=$\sqrt{21}$．