
| A. | p∧q | B. | p∨q | C. | (¬p)∧(¬q) | D. | p∨(¬q) |
分析 命题p:函数f(x)=$|\frac{1}{2}cos2x-\frac{1}{2}sin2x|$=$\frac{\sqrt{2}}{2}$$|sin(2x-\frac{π}{4})|$的最小正周期为$\frac{π}{2}$;命题q:函数f(x)=ln$\frac{3+x}{3-x}$,由$\frac{3+x}{3-x}$>0,可得定义域为:(-3,3).又f(-x)=-f(x),因此函数f(x)是奇函数,其图象关于原点中心对称,利用复合命题真假的判定方法即可判断出结论.
解答 解:命题p:函数f(x)=|cos2x-sinxcosx-$\frac{1}{2}$|=$|\frac{1}{2}cos2x-\frac{1}{2}sin2x|$=$\frac{\sqrt{2}}{2}$$|sin(2x-\frac{π}{4})|$的最小正周期为$\frac{π}{2}$,因此是假命题;
命题q:函数f(x)=ln$\frac{3+x}{3-x}$,由$\frac{3+x}{3-x}$>0,化为(x+3)(x-3)<0,解得-3<x<3,
可得定义域为:(-3,3).又f(-x)=$ln\frac{3-x}{3+x}$=-ln$\frac{3+x}{3-x}$=-f(x),因此函数f(x)是奇函数,其图象关于原点中心对称,是真命题.
则下列命题是真命题的是p∨q.
故选:B.
点评 本题考查了函数的奇偶性、三角函数的周期性、倍角公式与和差公式、不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
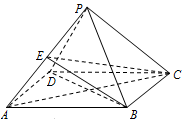 已知四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,$PA=\sqrt{6}$.
已知四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,$PA=\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -1 | C. | 2 | D. | $-1或\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验次数 |
| A | 甲 | 2次 | 6次 | 4次 | 12次 |
| B | 乙 | 3次 | 6次 | 3次 | 12次 |
| C | 丙 | 2次 | 2次 | 8次 | 12次 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com