练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知在正方体ABCD-A1B1C1D1中，点E是棱A1B1的中点，则直线AE与平面BDD1B1所成角的正切值是
     
    ．
    考点：直线与平面所成的角
    专题：空间角
    分析：首先利用转化法，求出线面所夹的角，进一步利用解三角形知识求出结果．
    解答： 解：已知在正方体ABCD-A1B1C1D1中，点E是棱A1B1的中点，
    连接AC交BD于O，做AB的中点F，连接B1F，取BO的中点G，连接FG，GB1
    所以：B1F∥AE，FG⊥BD，
    所以：AE与平面BDD1B1所成角为：∠FB1G
    设正方体的棱长为1，
    进一步求得：FG=
    		2
    4
    ，B1G=
    3
    		2
    4

    则：tan∠FB1G=
    FG
    B1G
    =
    1
    3

    故答案为：
    1
    3
    点评：本题考查的知识要点：线面的夹角问题，解三角形知识的应用，属于基础题型．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    己知向量
    m
    =（
    		3
    sin
    x
    4
    ，1），
    n
    =（cos
    x
    4
    ，cos2
    x
    4
    ），记f（x）=
    m
    •
    n
    ．
    （Ⅰ）若f（x）=1，求cos（
    2π
    3
    -x）的值；
    （Ⅱ）在锐角△ABC申，角A，B，C的对边分别是a，b，c，且满足（2a-c）cosB=bcosC，求函数f（A）的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    三个数a=0.22，b=log202，c=20.1之间的大小关系是（　　）
    A、a＜c＜b
    B、a＜b＜c
    C、b＜a＜c
    D、b＜c＜a

    查看答案和解析>>

    科目：高中数学 来源： 题型：

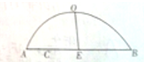    如图，A处为我军一炮兵阵地，距A处1000米的C处有一小山，山高为580米，在山的另一侧距C处3000米有敌武器库B，且A、B、C在同一水平直线删个，已知我炮兵轰击敌武器库是一段抛物线，这段抛物线的最大高度OE为800米．
    （1）求这条抛物线的方程；
    （2）问炮弹沿着这段话抛物线飞行是否会与小山碰撞？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数f（x）=x3-
    1
    2
    x2+bx+c在x=1时取得极值，且当x∈[-1，2]时，f（x）＜c2恒成立．
    （1）求实数b的值；
    （2）求实数c的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆的中心是坐标原点O，它的短轴长为2
    		2
    ，一个焦点F的坐标为（c，0）（c＞0），一个定点A的坐标为(
    10
    c
    -c，0)    ，且
    OF
    =2
    FA，
    过点A的直线与椭圆相交于P，Q两点：
    （1）求椭圆的方程和离心率；
    （2）如果OP⊥OQ，求直线PQ的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

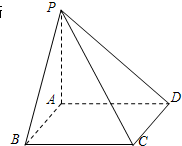    如图，已知四棱锥P-ABCD中，已知PA⊥底面ABCD，且底面ABCD为矩形，则下列结论中错误的是（　　）
    A、平面PAB⊥平面PAD
    B、平面PAB⊥平面PBC
    C、平面PBC⊥平面PCD
    D、平面PCD⊥平面PAD

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    ax2，x≤e
    lnx，x＞e.
    ，其中e是自然对数的底数，若直线y=2与函数y=f（x）的图象有三个交点，则常数a的取值范围是（　　）
    A、（-∞，2）
    B、（-∞，2]
    C、（2e-2，+∞）
    D、[2e-2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知|
    a
    |=4，|
    b
    |=3，（2
    a
    -3
    b
    ）•（2
    a
    +
    b
    ）=61．
    ①
    a
    与
    b
    的夹角；  
    ②求|
    a
    +
    b
    |和|
    a
    -
    b
    |．

    查看答案和解析>>

    同步练习册答案