
分析 (1)通过代入计算可知an+1=2an+2n+1,进而通过构造出首项、公差均为1的等差数列{$\frac{{a}_{n}}{{2}^{n}}$},计算即得结论;
(2)通过(1)可知cn=$\frac{1}{4}$-$\frac{1}{4({2}^{n+1}-1)}$,通过放缩可知$\frac{n}{4}$-$\frac{1}{7}$<c1+c2+…+cn<$\frac{n}{4}$(n>2),利用等价条件可n>$\frac{{2}^{10}}{7}$=146$\frac{2}{7}$,进而整理即得结论.
解答 解:(1)∵数列{an}满足an=f(2n)(n∈N+),
∴a1=f(2)=2,
又∵对任意α,β∈R,都有f(αβ)=αf(β)+βf(α),
∴an+1=f(2n+1)=2f(2n)+2nf(2)=2an+2n+1,
两边同时除以2n+1得:$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{{a}_{n}}{{2}^{n}}$=1,
∴数列{$\frac{{a}_{n}}{{2}^{n}}$}是首项、公差均为1的等差数列,
∴$\frac{{a}_{n}}{{2}^{n}}$=n,即an=n•2n;
(2)由(1)可知,bn=$\frac{{a}_{n}}{n}$($\frac{{a}_{n}}{n}$-1)=2n(2n-1),
cn=$\frac{{b}_{n}}{{b}_{n+1}}$=$\frac{{2}^{n}({2}^{n}-1)}{{2}^{n+1}({2}^{n+1}-1)}$=$\frac{{2}^{n+1}-2}{4({2}^{n+1}-1)}$=$\frac{1}{4}$-$\frac{1}{4({2}^{n+1}-1)}$<$\frac{1}{4}$,
∴c1+c2+…+cn<$\frac{n}{4}$,
∵cn=$\frac{1}{4}$-$\frac{1}{4({2}^{n+1}-1)}$=$\frac{1}{4}$-$\frac{1}{8•{2}^{n}-4}$=$\frac{1}{4}$-$\frac{1}{7•{2}^{n}+{2}^{n}-4}$,
∴cn=$\frac{1}{4}$-$\frac{1}{7•{2}^{n}+{2}^{n}-4}$>$\frac{1}{4}$-$\frac{1}{7•{2}^{n}}$(n>2),
∴c1+c2+…+cn>$\frac{n}{4}$-$\frac{1}{7}$•$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$=$\frac{n}{4}$-$\frac{1}{7}$+$\frac{1}{7•{2}^{n}}$>$\frac{n}{4}$-$\frac{1}{7}$(n>2),
∴$\frac{n}{4}$-$\frac{1}{7}$<c1+c2+…+cn<$\frac{n}{4}$(n>2),
∵不等式|Tn-$\frac{1}{4}$|<$\frac{1}{{2}^{10}}$恒成立等价于$\frac{1}{7n}$<$\frac{1}{{2}^{10}}$,等价于n>$\frac{{2}^{10}}{7}$=146$\frac{2}{7}$,
∴存在正整数M=146(或147,148,149,…),使得不等式|Tn-$\frac{1}{4}$|<$\frac{1}{{2}^{10}}$恒成立.
点评 本题是一道关于数列与不等式的综合题,涉及放缩法等基本技巧,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:解答题
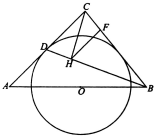 如图,等腰直角三角形ACB中,∠ACB=90°,圆心O为AB的中点,AC切圆O于点D.
如图,等腰直角三角形ACB中,∠ACB=90°,圆心O为AB的中点,AC切圆O于点D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{4}$) | B. | (-$\frac{1}{4}$,-$\frac{1}{8}$) | C. | (-$\frac{1}{8}$,-$\frac{1}{16}$) | D. | (-$\frac{1}{16}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com