
分析 先看函数的定义域是否关于原点对称,再看f(x)和f(-x)的关系,再根据奇函数、偶函数的定义得出结论.
解答 解:(1)∵f(x)=$\frac{\sqrt{1-{x}^{2}}}{|x+3|-3}$,
∴$\left\{\begin{array}{l}{1{-x}^{2}≥0}\\{|x+3|≠3}\end{array}\right.$,求得-1≤x≤1且x≠0,
故函数的定义域为[-1,0)∪(0,1].
∴f(x)=$\frac{\sqrt{{1-x}^{2}}}{x+3-3}$=$\frac{\sqrt{{1-x}^{2}}}{x}$,
再根据f(-x)=$\frac{\sqrt{{1-x}^{2}}}{-x}$=-f(x),可得函数f(x)为奇函数.
(2)∵f(x)=$\frac{|x|}{x}$(x-1)0 ,
故函数的定义域为{x|x≠0,且 x≠1},显然,函数的定义域不关于原点对称,
故函数f(x)为非奇非偶函数.
点评 本题主要考查函数的奇偶性的判断,属于基础题.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{2}$,$\frac{1}{2}$] | B. | [-$\frac{1}{2}$,0] | C. | [0,$\sqrt{6}$] | D. | [0,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 5$\sqrt{2}$ | C. | 2$\sqrt{5}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
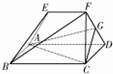 多面体ABCDFE中,底面四边形ABCD为矩形,EF∥AD,AE=FD,FG=GD,AD=2AB=2EF=2,且四边形EADF的面积为$\frac{3\sqrt{3}}{4}$.
多面体ABCDFE中,底面四边形ABCD为矩形,EF∥AD,AE=FD,FG=GD,AD=2AB=2EF=2,且四边形EADF的面积为$\frac{3\sqrt{3}}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com