
分析 (1)(i)根据导数的几何意义和最值和函数的单调性的关系即可求出,
(ii)构造函数,再分类讨论,根据导数和单调性的关系即可求出,
(2)依题意,不妨设x2>x1,求出f′($\frac{{{x_1}+{x_2}}}{2}$),构造函数令t=x2-x1>0,设$G(t)={e^{\frac{t}{2}}}-{e^{-\frac{t}{2}}}-t$,利用导数求出函数的单调性,即可证明.
解答 解:(1)(ⅰ)∵f'(x)=aex-1,$g'(x)=1-\frac{1}{x+1}({x>-1})$,
依题意,f(0)=0,且f(0)=0,解得a=1,b=-1,
∴f'(x)=ex-1,当f'(x)<0时,即x<0时,f(x)单调递减,
当f'(x)>0时,即x>0时,f(x)单调递增,
∴当x=0时,f(x)取得最小值0.
(ⅱ)由(ⅰ)知,f(x)≥0,即ex≥x+1,从而x≥ln(x+1),即g(x)≥0.
设F(x)=f(x)-kg(x)=ex+kln(x+1)-(k+1)x-1,
则$F'(x)={e^x}+\frac{k}{x+1}-({k+1})≥x+1+\frac{k}{x+1}-({k+1})$,
①当k=1时,因为x≥0,∴$F'(x)≥x+1+\frac{1}{x+1}-2≥0$(当且仅当x=0时等号成立),
此时F(x)在[0,+∞)上单调递增,
从而F(x)≥F(0)=0,即f(x)≥kg(x).
②当k<1时,由于g(x)≥0,∴g(x)≥kg(x),
又由(1)知f(x)-g(x)≥0,∴f(x)≥g(x)≥kg(x),
故F(x)≥0,
即f(x)≥kg(x).
③当k>1时,令h(x)=ex+$\frac{k}{x+1}$-(k+1),则$h'(x)={e^x}-\frac{k}{{{{({x+1})}^2}}}$,
显然h′(x)在[0,+∞)上单调递增,又$h'(0)=1-k<0,h'({\sqrt{k}-1})={e^{\sqrt{k}-1}}-1>0$,
∴h′(x)在$({0,\sqrt{k}-1})$上存在唯一零点,
当x∈(0,x0)时,h′(x)<0,∴h(x)在[0,x0]上单调递减,
从而F(x)<F(0)=0,即F′(x)<0,
∴F(x)在[0,x0]上单调递减,
从而当x∈(0,x0)时,F(x)<F(0)=0,即f(x)<kg(x),不合题意.
综上,实数k的取值范围为(-∞,1].
(2)证明:依题意,不妨设x2>x1,有$a{e^{x_2}}+b={x_2}$,$a{e^{x_1}}+b={x_1}$,
两式相减得:$a({e^{x_2}}-{e^{x_1}})={x_2}-{x_1}$,
整理得${x_2}-{x_1}=a({e^{x_2}}-{e^{x_1}})$,${e^{x_2}}-{e^{x_1}}>0$
则$\frac{{{x_2}-{x_1}}}{{{e^{x_2}}-{e^{x_1}}}}=a$,
于是$f'(\frac{{{x_1}+{x_2}}}{2})=a{e^{\frac{{{x_2}+{x_1}}}{2}}}-1=\frac{{{x_2}-{x_1}}}{{{e^{x_2}}-{e^{x_1}}}}•{e^{\frac{{{x_2}+{x_1}}}{2}}}-1=\frac{{{x_2}-{x_1}}}{{{e^{\frac{{{x_2}-{x_1}}}{2}}}-{e^{-\frac{{{x_2}-{x_1}}}{2}}}}}-1$,
令t=x2-x1>0,
则设$G(t)={e^{\frac{t}{2}}}-{e^{-\frac{t}{2}}}-t$,
则$G'(t)=\frac{1}{2}{e^{\frac{t}{2}}}+\frac{1}{2}{e^{-\frac{t}{2}}}-1>\frac{1}{2}•2•\sqrt{{e^{\frac{t}{2}}}•{e^{-\frac{t}{2}}}}-1=0$,
∴y=G(t)在(0,+∞)上单调递增,
则$G(t)={e^{\frac{t}{2}}}-{e^{-\frac{t}{2}}}-t>G(0)=0$,
于是有${e^{\frac{t}{2}}}-{e^{-\frac{t}{2}}}>t$,
即$\frac{{{x_2}-{x_1}}}{{{e^{\frac{{{x_2}-{x_1}}}{2}}}-{e^{-\frac{{{x_2}-{x_1}}}{2}}}}}<1$,
∴$f'(\frac{{{x_1}+{x_2}}}{2})=a{e^{\frac{{{x_2}+{x_1}}}{2}}}-1<0$.
即f′($\frac{{{x_1}+{x_2}}}{2}$)<0.
点评 本题考查了导数和函数的单调性以及和最值的关系,考查了运算能力,转化能力,解决问题的能力,属于难题.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | $\sqrt{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
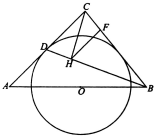 如图,等腰直角三角形ACB中,∠ACB=90°,圆心O为AB的中点,AC切圆O于点D.
如图,等腰直角三角形ACB中,∠ACB=90°,圆心O为AB的中点,AC切圆O于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 类别 | 有责任 | 无责任 | 总计 |
| 有酒精 | 650 | 150 | 800 |
| 无酒精 | 700 | 500 | 1200 |
| 合计 | 1350 | 650 | 2000 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{4}$) | B. | (-$\frac{1}{4}$,-$\frac{1}{8}$) | C. | (-$\frac{1}{8}$,-$\frac{1}{16}$) | D. | (-$\frac{1}{16}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈N*,3x2-2x+5<lnx | B. | ?x∈N*,3x2-2x+5≤lnx | ||
| C. | ?x∈N*,3x2-2x+5<lnx | D. | ?x∈N*,3x2-2x+5≤lnx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com