练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．已知命题p：?x∈N*，3x2-2x+5＞lnx，则￢p为（　　）
    A．?x∈N*，3x2-2x+5＜lnxB．?x∈N*，3x2-2x+5≤lnx
    C．?x∈N*，3x2-2x+5＜lnxD．?x∈N*，3x2-2x+5≤lnx

    分析 利用全称命题的否定是特称命题写出结果即可．

    解答 解：因为全称命题的否定是特称命题，所以，命题p：?x∈N*，3x2-2x+5＞lnx，则￢p为：?x∈N*，3x2-2x+5≤lnx．
    故选：D．

    点评 本题考查命题的否定，全称命题与特称命题的否定关系，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=aex-x+b，g（x）=x-ln（x+1），（a，b∈R，e为自然对数的底数）．
    （1）若曲线y=f（x）与y=g（x）在坐标原点处的切线相同，问：
    （ⅰ）求f（x）的最小值；
    （ⅱ）若x≥0时，f（x）≥kg（x）恒成立，试求实数k的取值范围；
    （2）若f（x）有两个不同的零点x1，x2，对任意a∈（0，+∞），b∈R，证明：f′（$\frac{{{x_1}+{x_2}}}{2}$）＜0（f′（x）为f（x）的导函数）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知平面向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-2，k），若$\overrightarrow{a}$与$\overrightarrow{b}$共线，则|$\overrightarrow{a}$+$\overrightarrow{b}$|=（　　）
    A．5B．5$\sqrt{2}$C．2$\sqrt{5}$D．$\sqrt{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．由下面样本数据利用最小二乘法求出的线性回归方程是$\widehat{y}$=0.7x+m，则实数m=0.35．
    x3456
    y2.5344.5

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．一个几何体的三视图为如图所示的三个直角三角形，则该几何体表面的直角三角形的个数为4个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的渐近线分别为l1，l2，直线l：y=-x+c过双曲线C的右焦点F（c，0），且分别与直线l1，l2交于A，B两点，若$\overrightarrow{FA}$=$\overrightarrow{AB}$，则双曲线C的离心率为（　　）
    A．$\sqrt{10}$B．2$\sqrt{2}$C．4D．$\frac{\sqrt{10}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

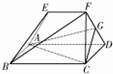    14．多面体ABCDFE中，底面四边形ABCD为矩形，EF∥AD，AE=FD，FG=GD，AD=2AB=2EF=2，且四边形EADF的面积为$\frac{3\sqrt{3}}{4}$．
    （1）判断直线BF与平面ACG的关系，并说明理由；
    （2）若平面EADF⊥平面ABCD，求平面FBC与平面ACG形成的锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．下列判断中错误的是（　　）
    A．若ξ～B（4，0.25），则Dξ=1
    B．“am2＜bm2”是“a＜b”的充分不必要条件
    C．若p、q均为假命题，则“p且q”为假命题
    D．命题“?x∈R，x2-x-1≤0”的否定是“?x0∈R，x02-x0-1＞0”

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．某统计部门随机抽查了3月1日这一天新世纪百货童装部100名顾客的购买情况，得到如图数据统计表，已知购买金额在2000元以上（不含2000元）的频率为0.4．
    购买金额频数频率
    （0，500]50.05
    （500，1000]xp
    （1000，1500]150.15
    （1500，2000]250.25
    （2000，2500]300.3
    （2500，3000]yq
    合计1001.00
    （1）确定x，y，p，q的值；
    （2）为进一步了解童装部的购买情况是否与顾客性别有关，对这100名顾客调查显示：购物金额在2000元以上的顾客中女顾客有35人，购物金额在2000元以下（含2000元）的顾客中男顾客有20人；
    ①请将列联表补充完整：
    女顾客男顾客合计
    购物金额在2000元以上35
    购物金额在2000元以下20
    合计100
    ②并据此列联表，判断是否有97.5%的把握认为童装部的购买情况与顾客性别有关？
    参考数据：
    P（K2≥k）0.010.050.0250.01
    k2.7063.8415.0246.635
    ${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$．

    查看答案和解析>>

    同步练习册答案