
���� ��ϵͳ������ÿ�����屻�鵽�ĸ�������жϢ٣�����ϵͳ������������֪�����ǵȾ������ԭ����һ���Ȳ����У����ĸ�ְ���ĺ����С����ɵȲ����У�������ʽ��ϵ���������������һ��ְ���ı���жϢڣ������ÿ�����屻�鵽�ĸ��ʣ����øò�ĸ���������ÿ�����屻�鵽�ĸ����жϢۣ�����֪���ݵķ����������-3x1+5��-3x2+5������-3xn+5�ı����жϢܣ�
��� �⣺���ڢ٣����ݳ��������ʿ�֪���������ֳ�����ÿ������鵽�ĸ��ʶ�����ͬ���ʢ���ȷ��
���ڢڣ��������л���һ��ְ���ı����x�ţ�����ϵͳ����������ĸ�ְ���ĺ����С�������У�6�š�x�š�32�š�45�ţ����ǹ��ɵȲ����У�
��6+45=x+32����x=6+45-32=19����ˣ���һ��ְ���ı��Ϊ19�ţ��ʢ���ȷ��
���ڢۣ�ÿ�����屻�鵽�ĸ��ʵ���$\frac{100}{600}=\frac{1}{6}$�����е������ͥӦ��ȡ360��$\frac{1}{6}$=60���ʢ���ȷ��
���ڢܣ�������x1��x2������xn��ƽ����Ϊ$\overline{x}$����$\overline{x}=\frac{1}{n}$��x1+x2+��+xn ����
������-3x1+5��-3x2+5������-3xn+5��ƽ����Ϊ$\frac{1}{n}$��-3x1+5-3x2+5+��-3xn+5 ��=$-\frac{3}{n}$��x1+x2+��+xn ��+5=-3$\overline{x}$+5��
�ɷ���Ĺ�ʽS2=$\frac{1}{n}$[��x1-$\overline{x}$��2+��x2-$\overline{x}$��2+��+��xn-$\overline{x}$��2]����֪������-3x1+5��-3x2+5������-3xn+5�ķ���Ϊ����x1��x2������xn�ķ����32=9������9��4=36��
��-3x1+5��-3x2+5������-3xn+5�ı���Ϊ$\sqrt{36}=6$���ʢ���ȷ��
�ʴ�Ϊ���٢ڢۢܣ�
���� ���⿼�����������ж���Ӧ�ã�������ϵͳ������ֲ������������һ�����ݷ���������е��⣮


 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
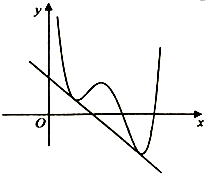 ��ͼ����ֱ֪��y=kx+m������y=f��x�����������㣬��F��x��=f��x��-kx�У�������
��ͼ����ֱ֪��y=kx+m������y=f��x�����������㣬��F��x��=f��x��-kx�У�������| A�� | 1������ֵ�㣬2����Сֵ�� | B�� | 2������ֵ�㣬1����Сֵ�� | ||
| C�� | 3������ֵ�㣬��Сֵ�� | D�� | 3����Сֵ�㣬����ֵ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com