
| A. | 若直线l∥平面α,直线l∥平面β,则α∥β | |
| B. | 若直线l⊥平面α,平面α⊥平面β,则l∥平面β | |
| C. | “两直线l1,l2,与同一平面α所成角相等”的充分不必要条件是“l1∥l2” | |
| D. | 若直线l上不同两点A,B到平面α的距离相等,则l∥α. |
分析 对于A,若直线l∥平面α,直线l∥平面β,则α∥β或α与β相交;
对于B,l在平面β内时,结论不成立;
对于C,与同一平面所成角相等的两条直线的位置关系可以是相交、平行与异面;若l1∥l2,则两直线l1,l2,与同一平面α所成角相等;
对于D,若l上两个点A、B满足线段AB的中点在平面内,则A、B到α的距离相等,但l与α相交.
解答 解:对于A,若直线l∥平面α,直线l∥平面β,则α∥β或α与β相交,故不正确;
对于B,l⊥平面α,且l不在平面β内,α⊥β,则必有l∥β成立,故不正确;
对于C,与同一平面所成角相等的两条直线的位置关系可以是相交、平行与异面;若l1∥l2,则两直线l1,l2,与同一平面α所成角相等,故正确;
对于D,若l上两个点A、B满足线段AB的中点在平面内,则A、B到α的距离相等,但l与α相交,故不正确.
故选:C.
点评 本题考查空间中直线与平面之间的位置关系,解题的关键是熟练掌握空间中线线平行、面面平行、线面平行的条件及有着较强的空间想像能力,考查了推理判断的能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在几何图形ABCDEF中,AB∥CD,AD=DC=CB=CF=1,∠ABC=60°,四边形ACEF为矩形,平面ACEF⊥平面ABCD.
如图,在几何图形ABCDEF中,AB∥CD,AD=DC=CB=CF=1,∠ABC=60°,四边形ACEF为矩形,平面ACEF⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3) | B. | (-∞,1) | C. | (-3,1) | D. | (-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
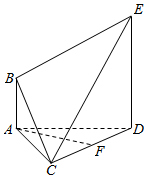 在如图所示的多面体ABCDE中,AB∥DE,AB⊥AD,△ACD是正三角形,AD=DE=2AB=2,$BC=\sqrt{5}$,F是CD的中点.
在如图所示的多面体ABCDE中,AB∥DE,AB⊥AD,△ACD是正三角形,AD=DE=2AB=2,$BC=\sqrt{5}$,F是CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com