
分析 由题意,①将函数化简,求出其最小值;
②即函数f(x)在定义域内为凹函数,结合函数图象,确定其凹凸性;
③将不等式因式分解,讨论根的大小,确定解集;
④根据已知条件,求出因变量的值,利用函数单调性比较函数值的大小.
解答 解:由题意,因为①f(x)=(x-sinα)2-9sin2α≥-9,所以①正确;
②对任意两实数x1、x2,都有f($\frac{{x}_{1}+{x}_{2}}{2}$)≤$\frac{f({x}_{1})+f({x}_{2})}{2}$即函数f(x)在定义域内为凹函数,
由①可知f(x)是以x=sinα为对称轴,开口向上的抛物线,所以是凹函数,
所以②正确;
③f(x)<0即x2-(2sinα)x-8sin2α<0,
所以(x-4sinα)(x+2sinα)<0,
所以当sinα>0时,解集为(-2sinα,4sinα),
当sinα<0时,解集为(4sinα,-2sinα),
所以③错;
④当2kπ<α<2kπ+π且α≠2kπ+$\frac{π}{2}$时,0<sinα<1,所以[sinα]=0,
所以{sinα}=sinα-[sinα]=sinα,
所以f([sinα])=f(0),f({sinα})=f(sinα),
又因为f(x)的对称轴为x=sinα且开口向上,所以f(0)>f(sinα),所以f([sinα])>f({sinα}),
所以④错.
故答案为①②.
点评 本题①主要利用二次函数性质以及三角函数值域,属于常见提醒;②中难点在于理解函数凹凸性的数学表达形式,也是解题关键;③中易错点是sinα的取值范围是[-1,1],需要讨论其正负性,解集会不同;④给出了新的概念,对学生综合素质要求较高,以函数单调性比较大小为知识框架,需要学生灵活掌握高斯函数性质及三角函数值域问题,综合性较强.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{4}$ | B. | -$\frac{8}{9}$ | C. | $\frac{3}{4}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若直线l∥平面α,直线l∥平面β,则α∥β | |
| B. | 若直线l⊥平面α,平面α⊥平面β,则l∥平面β | |
| C. | “两直线l1,l2,与同一平面α所成角相等”的充分不必要条件是“l1∥l2” | |
| D. | 若直线l上不同两点A,B到平面α的距离相等,则l∥α. |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
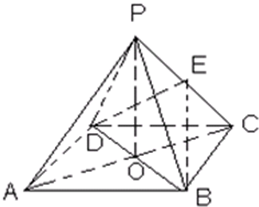 如图,ABCD是边长为1的正方形,O是正方形的中心,PO⊥底面ABCD,PO=1,E是PC的中点. 求证:
如图,ABCD是边长为1的正方形,O是正方形的中心,PO⊥底面ABCD,PO=1,E是PC的中点. 求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com