
分析 由已知得m=0,f(x)=2|x|-1,从而x∈(-∞,0)时,f(x)是减函数,x∈(0,+∞)时,f(x)是增函数,由此能比较a,b,c的大小关系.
解答 解:∵定义在R上的函数f(x)=2|x-m|-1(m为实数)为偶函数,
∴m=0,f(x)=2|x|-1,
∴x∈(-∞,0)时,f(x)是减函数,x∈(0,+∞)时,f(x)是增函数,
∵-1<log0.52<log0.53<log0.51=0,
log25>log24=2,
∴a=f(log0.53)=${2}^{|lo{g}_{0.5}3|}$-1∈(0,1),
b=f(log25)=${2}^{|lo{g}_{2}5|}$-1=4,
c=f(2m)=2|0|-1=0,
∴a,b,c的大小关系为b>a>c.
故答案为:b>a>c.
点评 本题考查三个数的大小的比较,是基础题,解题时要认真审题,注意偶函数性质、对数性质及运用法则合理运用.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [0,1) | [1,2) | [2,3) | [3,4) | [4,5) |
| 频数 | 3 | 15 | 24 | 12 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1} | B. | {1} | C. | {-1,1} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
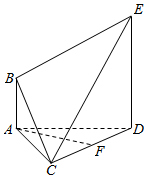 在如图所示的多面体ABCDE中,AB∥DE,AB⊥AD,△ACD是正三角形,AD=DE=2AB=2,$BC=\sqrt{5}$,F是CD的中点.
在如图所示的多面体ABCDE中,AB∥DE,AB⊥AD,△ACD是正三角形,AD=DE=2AB=2,$BC=\sqrt{5}$,F是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
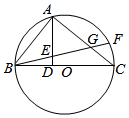 如图,BC是圆O的直径,点F在弧BC上,点A为劣弧$\widehat{BF}$的中点,作AD⊥BC于点D,BF与AD交于点E,与AC交于点G.
如图,BC是圆O的直径,点F在弧BC上,点A为劣弧$\widehat{BF}$的中点,作AD⊥BC于点D,BF与AD交于点E,与AC交于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com