Question

7．某微信群共有60人（不包括群主），春节期间，群主发60个随机红包（即每个人抢到的红包中的钱数是随机的，且每人只能抢一个）．红包被一抢而空．据统计，60个红包中钱数（单位：元）分配如表：

分组	[0，1）	[1，2）	[2，3）	[3，4）	[4，5）
频数	3	15	24	12	6

（Ⅰ）在表中作出这些数据的频率分布直方图；
（Ⅱ）估计红包中钱数的平均数及中位数；
（Ⅲ）若该群中成员甲、乙二人都抢到4.5元红包，现系统将从抢到4元及以上红包的人中随机抽取2人给群中每个人拜年，求甲、乙二人至少有一人被选中的概率．

Answer 1

分析 （Ⅰ）由已知作出频率分布表，由此作出频率分布直方图．
（Ⅱ）由频率分布直方图，估计红包中钱数的平均数和中位数．
（Ⅲ）该群中抢到红包的钱数不小于4元的人数是6；记为：a，b，c，d，甲，乙，由此利用列举法能求出甲、乙二人至少有一人被选中的概率．

解答 解：（Ⅰ）由已知作出频率分布表：

分组	[0，1）	[1，2）	[2，3）	[3，4）	[4，5）
频数	3	15	24	12	6
频率	0.05	0.25	0.4	0.2	0.1

由此作出频率分布直方图如下：

（Ⅱ）由频率分布直方图，估计红包中钱数的平均数为：
$\overline x=0.5×0.05+1.5×0.25+2.5×0.40+3.5×0.20+4.5×0.10$=2.55（元）
设中位数为x，则0.05+0.25+（x-2）×0.40=0.5，
解得中位数x=2.5（元）
（Ⅲ）该群中抢到红包的钱数不小于4元的人数是6；记为：a，b，c，d，甲，乙
现从这6人中随机抽取2人，基本事件数是：ab，ac，ad，a甲，a乙，bc，bd，b甲，
b乙，cd，c甲，c乙；d甲，d乙，甲乙共15种                                    
其中甲、乙二人至少有一人被选中的基本事件为：
a甲，a乙，b甲，b乙，c甲，c乙，d甲，d乙，甲乙，共9种，
所以对应的概率为：$P=\frac{9}{15}=\frac{3}{5}$．

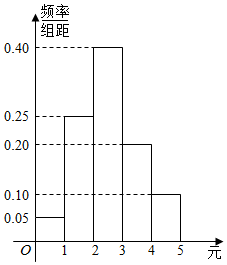
点评 本题考查频率分布直方图的作法及应用，概率的求法，是中档题，解题时要认真审题，注意列举法的合理运用．