
分析 (I)由已知中侧面积和底面积的单位建造成本,结合圆柱体的侧面积及底面积公式,根据该蓄水池的总建造成本为10800π元,构造方程整理后,可将V表示成r的函数,进而根据实际中半径与高为正数,得到函数的定义域;
(Ⅱ)根据(I)中函数的定义值及解析式,利用导数法,可确定函数的单调性,根据单调性,可得函数的最大值点.
解答 解:(Ⅰ)∵蓄水池的侧面积的建造成本为100•πrh元,
底面积成本为100πr2元,
∴蓄水池的总建造成本为100•πrh+100πr2元
即100•πrh+100πr2=10800π,
∴h=$\frac{1}{r}$(108-r2)
∴V(r)=πr2h=πr2•$\frac{1}{r}$(108-r2)=π(108r-r3)
又由r>0,h>0可得0<r<6$\sqrt{3}$
故函数V(r)的定义域为(0,6$\sqrt{3}$)
(Ⅱ)由(Ⅰ)中V(r)=π(108r-r3),(0<r<6$\sqrt{3}$)
可得V′(r)=π(108-3r2),(0<r<6$\sqrt{3}$)
∵令V′(r)=π(108-3r2)=0,则r=6
∴当r∈(0,6)时,V′(r)>0,函数V(r)为增函数
当r∈(6,6$\sqrt{3}$)时,V′(r)<0,函数V(r)为减函数
且当r=6,h=12时该蓄水池的体积最大
点评 本题考查的知识点是函数模型的应用,其中(Ⅰ)的关键是根据已知,求出函数的解析式及定义域,(Ⅱ)的关键是利用导数分析出函数的单调性及最值点.


科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | (0,1) | C. | ($\frac{1}{2}$,1) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
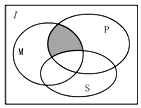
| A. | (M∩P)∪S | B. | (M∩P)∩S | C. | (M∩P)∩(∁IS) | D. | (M∩P)∪(∁IS) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com