
分析 由已知结合已知角的范围求得sin(α+β),cosα的值,再由cosβ=cos[(α+β)-α],展开两角差的余弦得答案.
解答 解:∵α,β均为锐角,∴0<α+β<π.
又cos(α+β)=-$\frac{11}{14}$,∴$\frac{π}{2}<α+β<π$,且$sin(α+β)=\sqrt{1-(-\frac{11}{14})^{2}}=\frac{5\sqrt{3}}{14}$.
∵sinα=$\frac{4\sqrt{3}}{7}$,∴$cosα=\sqrt{1-(\frac{4\sqrt{3}}{7})^{2}}=\frac{1}{7}$.
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα
=$-\frac{11}{14}×\frac{1}{7}+\frac{5\sqrt{3}}{14}×\frac{4\sqrt{3}}{7}=\frac{1}{2}$.
点评 本题考查两角和与差的余弦,关键是“拆角配角”思想的应用,是基础题.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:选择题
| A. | 1006 | B. | 1007 | C. | 1008 | D. | 1009 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 16 | 10 | 8.34 | 8.1 | 8.01 | 8 | 8.01 | 8.04 | 8.08 | 8.6 | 10 | 11.6 | 15.14 | … |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 日晷,是中国古代利用日影测得时刻的一种计时工具,又称“日规”.其原理就是利用太阳的投影方向来测定并划分时刻.利用日晷计时的方法是人类在天文计时领域的重大发明,这项发明被人类沿用达几千年之久.如图是故宫中的一个日晷,则根据图片判断此日晷的侧(左)视图可能为 ( )
日晷,是中国古代利用日影测得时刻的一种计时工具,又称“日规”.其原理就是利用太阳的投影方向来测定并划分时刻.利用日晷计时的方法是人类在天文计时领域的重大发明,这项发明被人类沿用达几千年之久.如图是故宫中的一个日晷,则根据图片判断此日晷的侧(左)视图可能为 ( )| A. |  | B. | 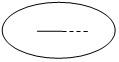 | C. | 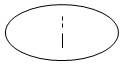 | D. | 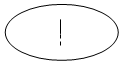 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com