
分析 当n=1时,a1=S1,当n≥2时,an=Sn-Sn-1,再检验n=1时是否适合n≥2时的关系式,以判断是合并在一起,还是分段表示.
解答 解:∵Sn=3n2-2n+2,
∴当n≥2时,an=Sn-Sn-1=(3n2-2n+2)-[3(n-1)2-2(n-1)+2]=6n-5,
当n=1时,a1=3×12-2×1+2=3,不适合上式;
∴an=$\left\{\begin{array}{l}{3,n=1}\\{6n-5,n≥2}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{3,n=1}\\{6n-5,n≥2}\end{array}\right.$.
点评 本题考查数列递推式,当n=1时,a1=S1,当n≥2时,an=Sn-Sn-1是解决问题之关键,考查推理与运算能力,属于中档题.


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
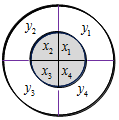 已知两个半径不等的圆盘叠放在一起(有一轴穿过它们的圆心),两圆盘上分别有互相垂直的两条直径将其分为四个区域,小圆盘上所写的实数分别记为x1,x2,x3,x4,大圆盘上所写的实数分别记为y1,y2,y3,y4,如图所示.将小圆盘逆时针旋转i(i=1,2,3,4)次,每次转动90°,记Ti(i=1,2,3,4)为转动i次后各区域内两数乘积之和,例如T1=x1y2+x2y3+x3y4+x4y1.若x1+x2+x3+x4<0,y1+y2+y3+y4<0,则以下结论正确的是( )
已知两个半径不等的圆盘叠放在一起(有一轴穿过它们的圆心),两圆盘上分别有互相垂直的两条直径将其分为四个区域,小圆盘上所写的实数分别记为x1,x2,x3,x4,大圆盘上所写的实数分别记为y1,y2,y3,y4,如图所示.将小圆盘逆时针旋转i(i=1,2,3,4)次,每次转动90°,记Ti(i=1,2,3,4)为转动i次后各区域内两数乘积之和,例如T1=x1y2+x2y3+x3y4+x4y1.若x1+x2+x3+x4<0,y1+y2+y3+y4<0,则以下结论正确的是( )| A. | T1,T2,T3,T4中至少有一个为正数 | B. | T1,T2,T3,T4中至少有一个为负数 | ||
| C. | T1,T2,T3,T4中至多有一个为正数 | D. | T1,T2,T3,T4中至多有一个为负数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com