
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (5,8) | B. | (8,+∞) | C. | ($\frac{13}{2}$,8) | D. | (5,$\frac{13}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 16 | 10 | 8.34 | 8.1 | 8.01 | 8 | 8.01 | 8.04 | 8.08 | 8.6 | 10 | 11.6 | 15.14 | … |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 日晷,是中国古代利用日影测得时刻的一种计时工具,又称“日规”.其原理就是利用太阳的投影方向来测定并划分时刻.利用日晷计时的方法是人类在天文计时领域的重大发明,这项发明被人类沿用达几千年之久.如图是故宫中的一个日晷,则根据图片判断此日晷的侧(左)视图可能为 ( )
日晷,是中国古代利用日影测得时刻的一种计时工具,又称“日规”.其原理就是利用太阳的投影方向来测定并划分时刻.利用日晷计时的方法是人类在天文计时领域的重大发明,这项发明被人类沿用达几千年之久.如图是故宫中的一个日晷,则根据图片判断此日晷的侧(左)视图可能为 ( )| A. |  | B. | 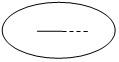 | C. | 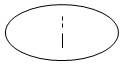 | D. | 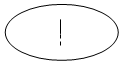 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com