
分析 本题是一个知道三角函数值及角的取值范围,求角的问题,由于本题中所涉及的角不是一个特殊角,故需要用反三角函数表示出答案
解答 解:由于arcsin$\frac{2}{5}$ 表示[-$\frac{π}{2}$,$\frac{π}{2}$]上正弦值等于$\frac{2}{5}$的一个锐角,
由$sinx=-\frac{2}{5}(π<x<\frac{3π}{2})$,则x=$π+arcsin\frac{2}{5}$,
故答案为:$π+arcsin\frac{2}{5}$.
点评 本题考查反三角函数的运用,解题的关键理解反三角函数的定义,用正确的形式表示出符号条件的角,本题重点是理解反三角函数定义,难点表示出符合条件的角,反三角函数在新教材省份已经不是高中数学学习内容.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
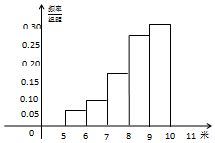 某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据整理后,分成六组得到频率分布直方图的一部分(如图).已知前五个小组的频率分别为0.06.0.10,0.14,0.28,0.30.第六小组的频数是6.
某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据整理后,分成六组得到频率分布直方图的一部分(如图).已知前五个小组的频率分别为0.06.0.10,0.14,0.28,0.30.第六小组的频数是6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com