
分析 m,n∈N*,f(x)=(1+x)m+(1+x)n展开式中x的系数为19,可得m+n=19.则当x2的系数=${∁}_{m}^{2}+{∁}_{n}^{2}$=n2-19n+171=$(n-\frac{19}{2})^{2}$+$\frac{323}{4}$.可得n=10或9时,x2的系数取得最小值.可得f(x)=(1+x)9+(1+x)10.再利用通项公式即可得出.
解答 解:m,n∈N*,f(x)=(1+x)m+(1+x)n展开式中x的系数为19,
∴m+n=19.
则当x2的系数=${∁}_{m}^{2}+{∁}_{n}^{2}$=$\frac{m(m-1)+n(n-1)}{2}$=$\frac{(19-n)(18-n)+n(n-1)}{2}$=n2-19n+171=$(n-\frac{19}{2})^{2}$+$\frac{323}{4}$.
∴n=10或9时,x2的系数最小为:81.
∴f(x)=(1+x)9+(1+x)10.
展开式中x7的系数=${∁}_{9}^{7}+{∁}_{10}^{7}$=156.
故答案为:156.
点评 本题考查了二项式定理的应用、二次函数的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 日晷,是中国古代利用日影测得时刻的一种计时工具,又称“日规”.其原理就是利用太阳的投影方向来测定并划分时刻.利用日晷计时的方法是人类在天文计时领域的重大发明,这项发明被人类沿用达几千年之久.如图是故宫中的一个日晷,则根据图片判断此日晷的侧(左)视图可能为 ( )
日晷,是中国古代利用日影测得时刻的一种计时工具,又称“日规”.其原理就是利用太阳的投影方向来测定并划分时刻.利用日晷计时的方法是人类在天文计时领域的重大发明,这项发明被人类沿用达几千年之久.如图是故宫中的一个日晷,则根据图片判断此日晷的侧(左)视图可能为 ( )| A. |  | B. | 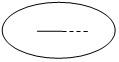 | C. | 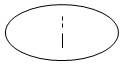 | D. | 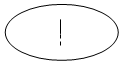 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com