
分析 (1)根据诱导公式化简可得f(α);
(2)利用同角三角函数关系式即可得解.
解答 解:(1)由$f(α)=\frac{{sin(α-\frac{π}{2})cos(\frac{3π}{2}+α)tan(π-α)}}{tan(-α-π)sin(-α-π)}$=$\frac{-cosαsinα•(-tanα)}{-tanα•sinα}$=-cosα.
(2)∵$f(α)=\frac{4}{5}$,即cosα=$-\frac{4}{5}$,
α为第三象限角,
那么:sin$α=-\sqrt{1-co{s}^{2}α}$=$-\frac{3}{5}$
可得$tanα=\frac{sinα}{cosα}=\frac{3}{4}$.
点评 本题主要考察了同角三角函数关系式和诱导公式的应用,属于基本知识的考查.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
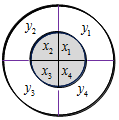 已知两个半径不等的圆盘叠放在一起(有一轴穿过它们的圆心),两圆盘上分别有互相垂直的两条直径将其分为四个区域,小圆盘上所写的实数分别记为x1,x2,x3,x4,大圆盘上所写的实数分别记为y1,y2,y3,y4,如图所示.将小圆盘逆时针旋转i(i=1,2,3,4)次,每次转动90°,记Ti(i=1,2,3,4)为转动i次后各区域内两数乘积之和,例如T1=x1y2+x2y3+x3y4+x4y1.若x1+x2+x3+x4<0,y1+y2+y3+y4<0,则以下结论正确的是( )
已知两个半径不等的圆盘叠放在一起(有一轴穿过它们的圆心),两圆盘上分别有互相垂直的两条直径将其分为四个区域,小圆盘上所写的实数分别记为x1,x2,x3,x4,大圆盘上所写的实数分别记为y1,y2,y3,y4,如图所示.将小圆盘逆时针旋转i(i=1,2,3,4)次,每次转动90°,记Ti(i=1,2,3,4)为转动i次后各区域内两数乘积之和,例如T1=x1y2+x2y3+x3y4+x4y1.若x1+x2+x3+x4<0,y1+y2+y3+y4<0,则以下结论正确的是( )| A. | T1,T2,T3,T4中至少有一个为正数 | B. | T1,T2,T3,T4中至少有一个为负数 | ||
| C. | T1,T2,T3,T4中至多有一个为正数 | D. | T1,T2,T3,T4中至多有一个为负数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
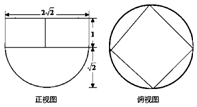
| A. | $2+\frac{{4\sqrt{2}π}}{3}$ | B. | $4+\frac{{8\sqrt{2}π}}{3}$ | C. | $2+\frac{{8\sqrt{2}π}}{3}$ | D. | $4+\frac{{4\sqrt{2}π}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 以直角三角形的一直角边为轴旋转所得的旋转体是圆锥 | |
| B. | 以直角梯形的一腰为轴旋转所得的旋转体是圆台 | |
| C. | 有一个面是多边形,其余各面都是三角形的几何体叫做棱锥 | |
| D. | 圆锥的侧面展开图为扇形,这个扇形的半径为圆锥底面圆的半径 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com