
【题目】已知函数![]()
(1)若函数![]() 在定义域上是增函数,求
在定义域上是增函数,求![]() 的取值范围;
的取值范围;
(2)若![]() 恒成立,求
恒成立,求![]() 的值.
的值.
【答案】(1) a![]() ;(2)a=1
;(2)a=1
【解析】
(1)若函数![]() 在定义域上是增函数.则
在定义域上是增函数.则![]()
![]() 恒成立,再变量分离求最值即可得解;(2)根据不等式恒成立,转化为最值问题,求出函数的导数,利用函数的单调性求最值即可.
恒成立,再变量分离求最值即可得解;(2)根据不等式恒成立,转化为最值问题,求出函数的导数,利用函数的单调性求最值即可.
(1)∵![]() ,∴
,∴![]()
∵![]() 在定义域上是单调增函数,∴当
在定义域上是单调增函数,∴当![]() 时,
时,![]() 恒成立,
恒成立,
∴![]() ,设
,设![]() >0,则
>0,则![]()
![]()
![]() 又
又![]()
所以a![]()
(2)(Ⅱ)f(x)≤ax恒成立等价于![]() ,f(x)﹣ax≤0恒成立.
,f(x)﹣ax≤0恒成立.
令![]() ,
,
则f(x)≤ax恒成立等价于![]() ,h(x)≤0=h(1)(*).
,h(x)≤0=h(1)(*).
要满足(*)式,即h(x)在x=1时取得最大值.
∵![]() .
.
由h'(1)=0解得a=1.
当a=1时,![]() ,
,
∴当![]() 时,h'(x)>0;当x∈(1,+∞)时,h'(x)<0.
时,h'(x)>0;当x∈(1,+∞)时,h'(x)<0.
∴当a=1时,h(x)在![]() 上单调递增,在(1,+∞)上单调递减,
上单调递增,在(1,+∞)上单调递减,
从而h(x)≤h(1)=0,符合题意.
所以,a=1.


科目:高中数学 来源: 题型:
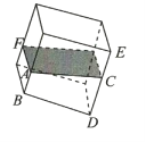
【题目】在一个长方体的容器中,里面装有少量的水,现在将容器绕着其底部的一条棱倾斜.
(1)在倾斜的过程中,水面的形状不断变化,可能是矩形,也可能变成不是矩形的平行四边形,对吗?
(2)在倾斜的过程中,水的形状也不断变化,可以是棱柱,也可能变为棱台或棱锥,对吗?
(3)如果倾斜时,不是绕着底部的一条棱,而是绕着其底面的一个顶点,上面的第(1)问和第(2)问对不对?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P与两个定点O(0,0),A(3,0)的距离的比值为2,点P的轨迹为曲线C.
(1)求曲线C的轨迹方程
(2)过点(﹣1,0)作直线与曲线C交于A,B两点,设点M坐标为(4,0),求△ABM面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在△![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点, ![]() ,
,![]() .将△
.将△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,
, ![]() 为
为![]() 的中点,如图2.
的中点,如图2.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求F到平面A1OB的距离.

图1 图2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为![]() 的直线l与抛物线C交于A,B两点,B在x轴的上方,且点B的横坐标为4.
的直线l与抛物线C交于A,B两点,B在x轴的上方,且点B的横坐标为4.
(1)求抛物线C的标准方程;
(2)设点P为抛物线C上异于A,B的点,直线PA与PB分别交抛物线C的准线于E,G两点,x轴与准线的交点为H,求证:HGHE为定值,并求出定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中
(1)在等差数列![]() 中,
中,![]() 是
是![]() 的充要条件;
的充要条件;
(2)已知等比数列![]() 为递增数列,且公比为
为递增数列,且公比为![]() ,若
,若![]() ,则当且仅当
,则当且仅当![]() ;
;
(3)若数列![]() 为递增数列,则
为递增数列,则![]() 的取值范围是
的取值范围是![]() ;
;
(4)已知数列![]() 满足
满足![]() ,则数列
,则数列![]() 的通项公式为
的通项公式为![]()
(5)若![]() 是等比数列
是等比数列![]() 的前
的前![]() 项的和,且
项的和,且![]() ;(其中
;(其中![]() 、
、![]() 是非零常数,
是非零常数,![]() ),则A+B为零.
),则A+B为零.
其中正确命题是_________(只需写出序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com