
分析 根据题意,分2种情况讨论:①、小刚与小红不相邻,②、小刚与小红相邻,由排列、组合公式分别求出每一种情况的排法数目,由分类加法原理计算可得答案.
解答 解:根据题意,分2种情况讨论:
①、小刚与小红不相邻,
将除小明、小刚、小红之外的2人全排列,有A22种安排方法,排好后有3个空位,
将小明与小刚看成一个整体,考虑其顺序,有A22种情况,
在3个空位中,任选2个,安排这个整体与小红,有A32种安排方法,
有A22×A32×A22=24种安排方法;
②、小刚与小红相邻,
则三人中小刚在中间,小明、小红在两边,有A22种安排方法,将三人看成一个整体,
将整个整体与其余2人进行全排列,有A33种安排方法,
此时有A33×A22=12种排法,
则共有24+12=36种安排方法;
故答案为:36.
点评 本题考查排列、组合的运用,注意特殊元素优先考虑,不同的问题利用不同的方法解决如相邻问题用捆绑,不相邻问题用插空等方法.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 0 | C. | 一$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
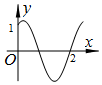
| A. | 函数f(x)的最小正周期是$\frac{12}{5}$ | |
| B. | 函数g(x)=$\frac{{2\sqrt{3}}}{3}sin\frac{5π}{6}$x的图象可由函数f(x)的图象向右平移$\frac{2}{5}$个单位得到 | |
| C. | 函数f(x)图象的一个对称中心是(-$\frac{4}{5}$,0) | |
| D. | 函数f(x)的一个递减区间是(5,$\frac{31}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
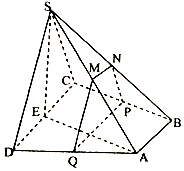 如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别与BC,AD交于点P,Q,若$\overrightarrow{DQ}$=t$\overrightarrow{DA}$.
如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别与BC,AD交于点P,Q,若$\overrightarrow{DQ}$=t$\overrightarrow{DA}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{3}{2}$ | B. | ±$\frac{2}{3}$ | C. | ±$\frac{3}{4}$ | D. | ±$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 50万元 | B. | 30万元 | C. | 25万元 | D. | 22万元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com