Question

6£®ÈçͼÊÇf£¨x£©=$\frac{{2\sqrt{3}}}{3}$cos£¨¦Øx+¦Õ£©£¨¦Ø£¾0£©µÄ²¿·ÖͼÏó£¬ÏÂÁÐ˵·¨´íÎóµÄÊÇ£¨¡¡¡¡£©

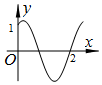
• A£® º¯Êýf£¨x£©µÄ×îСÕýÖÜÆÚÊÇ$\frac{12}{5}$
• B£® º¯Êýg£¨x£©=$\frac{{2\sqrt{3}}}{3}sin\frac{5¦Ð}{6}$xµÄͼÏó¿ÉÓɺ¯Êýf£¨x£©µÄͼÏóÏòÓÒƽÒÆ$\frac{2}{5}$¸öµ¥Î»µÃµ½
• C£® º¯Êýf£¨x£©Í¼ÏóµÄÒ»¸ö¶Ô³ÆÖÐÐÄÊÇ£¨-$\frac{4}{5}$£¬0£©
• D£® º¯Êýf£¨x£©µÄÒ»¸öµÝ¼õÇø¼äÊÇ£¨5£¬$\frac{31}{5}$£©

Answer 1

·ÖÎö ¸ù¾ÝͼÏó¹ý£¨0£¬1£©£¬£¨2£¬0£©Çó³ö¦Ø ºÍ¦Õ£¬¼´¿ÉÇóº¯Êýf£¨x£©µÄ½âÎöʽ£»¸ù¾Ýº¯Êý½âÎöʽ֮¼äµÄ¹ØϵÅжϸ÷Ñ¡Ïî¼´¿ÉµÃ½áÂÛ£®

½â´ð ½â£º¸ù¾ÝͼÏó¿ÉÖª£¬f£¨x£©=$\frac{{2\sqrt{3}}}{3}$cos£¨¦Øx+¦Õ£©£¨¦Ø£¾0£©µÄͼÏó¹ý£¨0£¬1£©£¬£¨2£¬0£©
¿ÉµÃ£ºf£¨0£©=$\frac{{2\sqrt{3}}}{3}$cos£¨¦Õ£©=1£¬½âµÃ£º¦Õ=$\frac{¦Ð}{6}$+2k¦Ð»ò¦Õ=-$\frac{¦Ð}{6}$+2k¦Ð£¬£¨k¡ÊZ£©
f£¨2£©=$\frac{{2\sqrt{3}}}{3}$cos£¨2¦Ø+$\frac{¦Ð}{6}$£©=0£¬½âµÃ¦Ø=$\frac{¦Ð}{6}$+k¦Ð»ò¦Ø=$\frac{¦Ð}{3}$+k¦Ð£®
µ±k=-1ʱ£¬|¦Ø|Ϊ£º$\frac{5¦Ð}{6}$£¬ÖÜÆÚT=$\frac{2¦Ð}{|-\frac{5¦Ð}{6}|}$=$\frac{12}{5}$£®¹ÊA¶Ô£®´Ëʱ¿ÉµÃf£¨x£©=$\frac{2\sqrt{3}}{3}$cos£¨$-\frac{5¦Ð}{6}x+\frac{¦Ð}{6}$£©£®
º¯Êýg£¨x£©=$\frac{{2\sqrt{3}}}{3}sin\frac{5¦Ð}{6}$xµÄͼÏóÏòÓÒƽÒÆ$\frac{2}{5}$¸öµ¥Î»¿ÉµÃ£º$\frac{2\sqrt{3}}{3}sin[\frac{5¦Ð}{6}£¨x-\frac{2}{5}£©]=\frac{2\sqrt{3}}{3}sin£¨\frac{5¦Ð}{6}x-\frac{¦Ð}{3}£©$=$\frac{2\sqrt{3}}{3}$cos£¨$-\frac{5¦Ð}{6}x+\frac{¦Ð}{6}$£©£®¹ÊB¶Ô£®
µ±x=-$\frac{4}{5}$ʱ£¬º¯Êýf£¨$-\frac{4}{5}$£©=$\frac{2\sqrt{3}}{3}$cos£¨$\frac{5¦Ð}{6}¡Á\frac{4}{5}+\frac{¦Ð}{6}$£©£®=$\frac{2\sqrt{3}}{3}¡Á\frac{\sqrt{3}}{2}$=1£¬¹ÊC²»¶Ô£®
ÓÉf£¨x£©=$\frac{2\sqrt{3}}{3}$cos£¨$-\frac{5¦Ð}{6}x+\frac{¦Ð}{6}$£©=$\frac{2\sqrt{3}}{3}$cos£¨$\frac{5¦Ð}{6}x-\frac{¦Ð}{6}$£©£®
Áî0+2k¦Ð¡Ü$\frac{5¦Ð}{6}x-\frac{¦Ð}{6}$£©¡Ü¦Ð+2k¦Ð£¬
¿ÉµÃ£º$\frac{1}{5}+\frac{12}{5}k¡Üx¡Ü\frac{7}{5}+\frac{12}{5}k$£¬£¨k¡ÊZ£©
µ±k=2ʱ£¬¿ÉµÃ$5¡Üx¡Ü\frac{31}{5}$Êǵ¥µ÷µÝ¼õ£®¹ÊD¶Ô£®
¹ÊÑ¡C£®

µãÆÀ ±¾ÌâÖ÷Òª¿¼²éÈý½Çº¯ÊýµÄͼÏóºÍÐÔÖÊ£¬¸ù¾ÝͼÏóÇó³öº¯ÊýµÄ½âÎöʽÊǽâ¾ö±¾ÌâµÄ¹Ø¼ü£®ÒªÇóÊìÁ·ÕÆÎÕº¯ÊýͼÏóÖ®¼äµÄ±ä»¯¹Øϵ£®