
已知函数 .
.
(1)若函数 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(2)若函数 在
在 上的最小值为3,求实数
上的最小值为3,求实数 的值.
的值.
(1)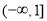 ,(2)
,(2)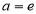 .
.
【解析】
试题分析:(1)利用导数研究函数单调性,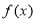 在
在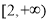 上是增函数就是
上是增函数就是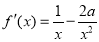 ≥0在
≥0在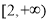 上恒成立,恒成立问题一般利用变量分离转化为最值问题,即
上恒成立,恒成立问题一般利用变量分离转化为最值问题,即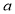 ≤
≤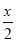 在
在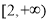 上恒成立.令
上恒成立.令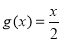 ,则
,则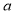 ≤
≤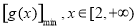 .∵
.∵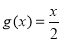 在
在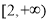 上是增函数,∴
上是增函数,∴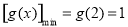 .∴
.∴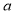 ≤1.所以实数
≤1.所以实数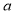 的取值范围为
的取值范围为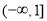 .(2)利用导数研究函数最值,实际还是研究函数单调性. ①若
.(2)利用导数研究函数最值,实际还是研究函数单调性. ①若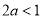 ,
,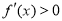 ,
,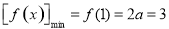 ,解得
,解得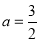 (舍去).②若
(舍去).②若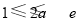 ,当
,当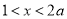 时,
时,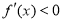 ,当
,当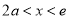 时,
时,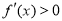 ,
,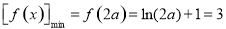 ,解得
,解得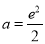 (舍去).③若
(舍去).③若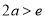 ,则
,则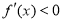 ,
,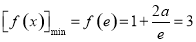 ,所以
,所以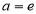 .
.
【解析】
(1)∵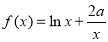 ,∴
,∴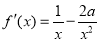 . 2分
. 2分
∵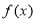 在
在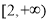 上是增函数,
上是增函数,
∴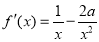 ≥0在
≥0在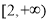 上恒成立,即
上恒成立,即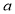 ≤
≤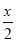 在
在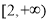 上恒成立. 4分
上恒成立. 4分
令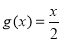 ,则
,则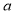 ≤
≤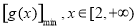 .
.
∵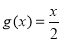 在
在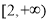 上是增函数,∴
上是增函数,∴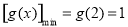 .
.
∴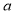 ≤1.所以实数
≤1.所以实数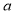 的取值范围为
的取值范围为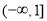 . 7分
. 7分
(2)由(1)得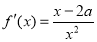 ,
,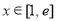 .
.
①若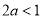 ,则
,则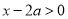 ,即
,即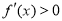 在
在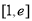 上恒成立,此时
上恒成立,此时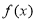 在
在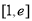 上是增函数.
上是增函数.
所以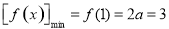 ,解得
,解得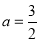 (舍去). 10分
(舍去). 10分
②若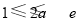 ,令
,令 ,得
,得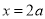 .当
.当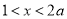 时,
时,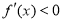 ,所以
,所以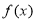 在
在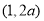 上是减函数,当
上是减函数,当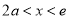 时,
时,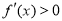 ,所以
,所以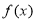 在
在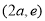 上是增函数.
上是增函数.
所以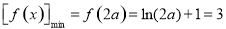 ,解得
,解得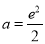 (舍去). 13分
(舍去). 13分
③若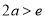 ,则
,则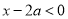 ,即
,即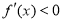 在
在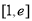 上恒成立,此时
上恒成立,此时 在
在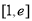 上是减函数.
上是减函数.
所以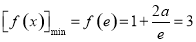 ,所以
,所以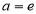 .------16分
.------16分
考点:利用导数研究函数单调性,利用导数研究函数最值.


科目:高中数学 来源:2015届江苏省无锡江阴市高二下学期期中考试理科数学试卷(解析版) 题型:填空题
航空母舰“辽宁舰”将进行一次编队配置科学实验,要求2艘攻击型核潜艇一前一后,2艘驱逐舰和2艘护卫舰分列左、右,同侧不能都是同种舰艇,则舰艇分配方案的方法数为________.(用数字作答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com