
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 5 | ﹣5 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为( ![]() ,0),求θ的最小值.
,0),求θ的最小值.
【答案】
(1)解:根据表中已知数据,解得A=5,ω=2,φ=﹣ ![]() .数据补全如下表:
.数据补全如下表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
|
|
|
|
Asin(ωx+φ) | 0 | 5 | 0 | ﹣5 | 0 |
且函数表达式为f(x)=5sin(2x﹣ ![]() )
)
(2)解:由(Ⅰ)知f(x)=5sin(2x﹣ ![]() ),得g(x)=5sin(2x+2θ﹣
),得g(x)=5sin(2x+2θ﹣ ![]() ).
).
因为y=sinx的对称中心为(kπ,0),k∈Z.
令2x+2θ﹣ ![]() =kπ,解得x=
=kπ,解得x= ![]() ,k∈Z.
,k∈Z.
由于函数y=g(x)的图象关于点( ![]() ,0)成中心对称,令
,0)成中心对称,令 ![]() =
= ![]() ,
,
解得θ= ![]() ,k∈Z.由θ>0可知,当K=1时,θ取得最小值
,k∈Z.由θ>0可知,当K=1时,θ取得最小值 ![]()
【解析】(1)根据表中已知数据,解得A=5,ω=2,φ=﹣ ![]() .从而可补全数据,解得函数表达式为f(x)=5sin(2x﹣
.从而可补全数据,解得函数表达式为f(x)=5sin(2x﹣ ![]() ).(2)由(Ⅰ)及函数y=Asin(ωx+φ)的图象变换规律得g(x)=5sin(2x+2θ﹣
).(2)由(Ⅰ)及函数y=Asin(ωx+φ)的图象变换规律得g(x)=5sin(2x+2θ﹣ ![]() ).令2x+2θ﹣
).令2x+2θ﹣ ![]() =kπ,解得x=
=kπ,解得x= ![]() ,k∈Z.令
,k∈Z.令 ![]() =
= ![]() ,解得θ=
,解得θ= ![]() ,k∈Z.由θ>0可得解.
,k∈Z.由θ>0可得解.


科目:高中数学 来源: 题型:
【题目】某省的一个气象站观测点在连续4天里记录的![]() 指数
指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() (单位:
(单位: ![]() )的情况如表1:
)的情况如表1:
|
| 700 |
|
|
| 0.5 | 3.5 | 6.5 | 9.5 |
该省某市2017年9月![]() 指数频数分布如表2:
指数频数分布如表2:
|
|
|
|
|
|
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设![]() ,根据表1的数据,求出
,根据表1的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)小李在该市开了一家洗车店,经统计,洗车店平均每天的收入与![]() 指数有相关关系,如表3:
指数有相关关系,如表3:
|
|
|
|
|
|
日均收入(元) |
|
|
|
|
|
根据表3估计小李的洗车店9月份平均每天的收入.
(附参考公式: ![]() ,其中
,其中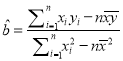 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,当x≥0时f(x)=2x﹣x2 ,
(1)求f(x)的表达式;
(2)设0<a<b,当x∈[a,b]时,f(x)的值域为 ![]() ,求a,b的值.
,求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=loga(x﹣3a)(a>0且a≠1),当点P(x,y)是函数y=f(x)图象上的点时,点
Q(x﹣2a,﹣y)是函数y=g(x)图象上的点.
(1)写出函数y=g(x)的解析式;
(2)若当x∈[a+2,a+3]时,恒有|f(x)﹣g(x)|≤1,试确定a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ax2﹣2ax+1+b(a>0)在区间[2,3]上有最大值4和最小值1.设f(x)= ![]() .
.
(1)求a、b的值;
(2)若不等式f(2x)﹣k2x≥0在x∈[﹣1,1]上恒成立,求实数k的取值范围;
(3)若f(|2x﹣1|)+k ![]() ﹣3k=0有三个不同的实数解,求实数k的取值范围.
﹣3k=0有三个不同的实数解,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com