
分析 先根据导数的运算法则求导,再代值计算即可.
解答 解:(1)f(x)=x•e2x+1+$\frac{lnx}{\sqrt{x}}$,(x0=1);
∴f′(x)=e2x+1+2x•e2x+1+$\frac{\frac{\sqrt{x}}{x}-\frac{1}{2}{x}^{-\frac{1}{2}}}{x}$,
∴f′(1)=3e3+$\frac{1}{2}$,
(2)f(x)=$\frac{tanx}{x}$,
∵(tanx)′=($\frac{sinx}{cosx}$)=$\frac{co{s}^{2}x+si{n}^{2}x}{co{s}^{2}x}$=$\frac{1}{co{s}^{2}x}$
∴f′(x)=$\frac{x(tanx)^{′}-tanx}{{x}^{2}}$=$\frac{\frac{x}{co{s}^{2}x}-tanx}{{x}^{2}}$,
∴f′($\frac{π}{4}$)=$\frac{8π-16}{{π}^{2}}$
点评 本题考查了导数的运算法则和导数值的求法,属于基础题.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:解答题
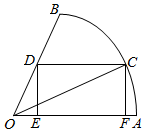 圆心角为60°的扇形AOB的半径为1,C是AB弧上一点,作矩形CDEF,如图,当C点在什么位置时,这个矩形的面积最大?这时的;∠AOC等于多少度?
圆心角为60°的扇形AOB的半径为1,C是AB弧上一点,作矩形CDEF,如图,当C点在什么位置时,这个矩形的面积最大?这时的;∠AOC等于多少度?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
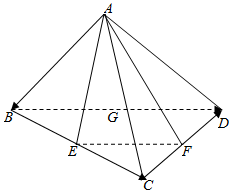 如图所示,已知空间四边形ABCD,连接AC,BD,E,F,G分别是BC,CD,DB的中点,请化简:
如图所示,已知空间四边形ABCD,连接AC,BD,E,F,G分别是BC,CD,DB的中点,请化简:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,1] | B. | [-3,3] | C. | (-∞,-3)∪(1,+∞) | D. | (-∞,-3)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com