Question

13．已知△AOB中，∠AOB=120°，|$\overrightarrow{OA}$|=3，|$\overrightarrow{OB}$|=2，过O作OD垂直AB于点D，点E为线段OD的中点，则$\overrightarrow{OE}$•$\overrightarrow{EA}$的值为（　　）

• A． $\frac{5}{19}$
• B． $\frac{27}{76}$
• C． $\frac{3}{76}$
• D． $\frac{3}{19}$

Answer 1

分析 由题意画出图形，建立如图所示坐标系，利用坐标求解．

解答 解：由题意建立如图所示坐标系．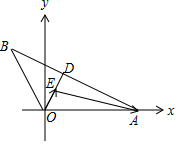

A（3，0），B（-1，$\sqrt{3}$），设D（x，y），
由$\overrightarrow{AD}=λ\overrightarrow{AB}$，可得（x-3，y）=λ（-4，$\sqrt{3}$），
即$\left\{\begin{array}{l}{x-3=-4λ}\\{y=\sqrt{3}λ}\end{array}\right.$，得D（3-4λ，$\sqrt{3}λ$）．
由$\overrightarrow{OD}•\overrightarrow{AB}=（3-4λ，\sqrt{3}λ）•（-4，\sqrt{3}）=0$，
得-4（3-4λ）+3λ=0，即$λ=\frac{12}{19}$．
∴D（$\frac{9}{19}，\frac{12\sqrt{3}}{19}$），则E（$\frac{9}{38}，\frac{6\sqrt{3}}{19}$），
∴$\overrightarrow{EA}=（\frac{105}{38}，-\frac{6\sqrt{3}}{19}）$，
则$\overrightarrow{OE}•\overrightarrow{EA}=（\frac{9}{38}，\frac{6\sqrt{3}}{19}）•（\frac{105}{38}，-\frac{6\sqrt{3}}{19}）$=$\frac{9×105}{3{8}^{2}}-\frac{6\sqrt{3}×6\sqrt{3}}{19×19}=\frac{27}{76}$．
故选：B．

点评 本题考查平面向量的数量积运算，考查数量积的坐标运算，建立平面直角坐标系起到事半功倍的效果，是中档题．