
| ����x��Ԫ�� | 18 | 19 | 20 | 21 | 22 |
| ����y���ᣩ | 61 | 56 | 50 | 48 | 45 |
���� 1������ƽ���������ù�ʽ���a��b�����ɵó�y��x�Ļع�ֱ�߷��̣�
��2�����õ�����ΪzԪ����������=��������-�ɱ������������������䷽�������õ��������
��� �⣺��1����$x=\frac{18+19+20+21+22}{5}=20��y=\frac{61+56+50+48+45}{5}=52$��
$s_y^2=\frac{1}{5}��{{9^2}+{4^2}+{2^2}+{4^2}+{7^2}}��=33.2$��
��$\sum_{i=1}^5{��{{x_i}-x}��}��{{y_i}-y}��=-40��{\sum_{i=1}^5{��{{x_i}-x}��}^2}=10$��
��$b=\frac{{\sum_{i=1}^5{��{{x_i}-x}��}��{{y_i}-y}��}}{{{{\sum_{i=1}^5{��{{x_i}-x}��}}^2}}}=-4��\widehata=y-\widehatbx=52+20��4=132$��
����y��x�Ļع�ֱ�߷���Ϊ��$\widehaty=-4\widehatx+132$��
��2����õ�����z=��x-14��y=-4x2+188x-1848��
�߶��κ���z=-4x2+188x-1848�Ŀ��ڳ��£�
�൱$x=\frac{188}{8}=23.5$ʱ��zȡ���ֵ��
�൱����Ӧ��Ϊ23.5Ԫʱ���ɻ���������
���� ������Ҫ����ع������������κ�������������������Ӧ����ʶ�������е��⣮


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
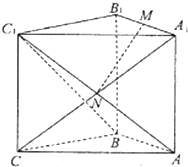 ֱ������ABC-A1B1C1�У���ABC=90�㣬AB=BC=BB1��MΪA1B1���е㣬N��AC1��A1C�Ľ��㣮
ֱ������ABC-A1B1C1�У���ABC=90�㣬AB=BC=BB1��MΪA1B1���е㣬N��AC1��A1C�Ľ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{5}$ | B�� | $\frac{2}{5}$ | C�� | $\frac{3}{4}$ | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����֪Բ�ڽ��ı���ABCD����T=tan$\frac{A}{2}$+tan$\frac{B}{2}$+tan$\frac{C}{2}$+tan$\frac{D}{2}$��
��ͼ��ʾ����֪Բ�ڽ��ı���ABCD����T=tan$\frac{A}{2}$+tan$\frac{B}{2}$+tan$\frac{C}{2}$+tan$\frac{D}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �۽������� | B�� | ��������� | C�� | ֱ�������� | D�� | ���������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com