Question

3．某校高一年级学生全部参加了体育科目的达标测试，现从中随机抽取40名学生的测试成绩，整理数据并按分数段[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]进行分组，假设同一组中的每个数据可用该组区间的中点值代替，则得到体育成绩的折线图（如下）

（Ⅰ）体育成绩大于或等于70分的学生常被成为“体育良好”，已知该校高一年级有1000名学生，试估计，高一全年级中“体育良好”的学生人数；
（Ⅱ）为分析学生平时的体育活动情况，现从体育成绩在[60，70）和[80，90）的样本学生中随机抽取2人，至少有1人体育成绩在[60，70）的概率；
（Ⅲ）假设甲、乙、丙三人的体育成绩分别为a，b，c，且分别在[70，80），[80，90），[90，100]三组中，其中a，b，c∈N，当数据a，b，c的方差s²最小时，写出a，b，c的值．（结论不要求证明）

Answer 1

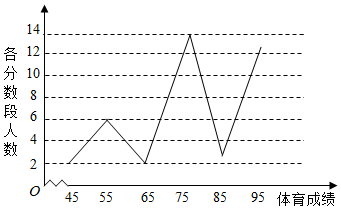
分析 （Ⅰ）由折线图求出样本中体育成绩大于或等于70分的学生人数，由此能求出高一全年级中“体育良好”的学生人数．
（Ⅱ）设“至少有1人体育成绩在（60，70）”为事件A，利用对立事件概率计算公式能求出至少有1人体育成绩在[60，70）的概率．
（Ⅲ）由题意，能写出数据a，b，c的方差s²最小时，a，b，c的值．

解答 解：（Ⅰ）由折线图，知样本中体育成绩大于或等于70分的学生有：14+3+13=30人，
∴高一全年级中“体育良好”的学生人数为：1000×$\frac{30}{40}$=750人．
（Ⅱ）设“至少有1人体育成绩在（60，70）”为事件A，
由题意，得P（A）=1-$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=1-$\frac{3}{10}$=$\frac{7}{10}$，
∴至少有1人体育成绩在[60，70）的概率为$\frac{7}{10}$．
（Ⅲ）由题意，当数据a，b，c的方差s²最小时，
a，b，c的值分别为79，84，90或79，85，90．

点评 本题考查折线图的应用，考查概率的求法，是基础题，解题时要认真审题，注意注意对立事件概率计算公式的合理运用．