
 如图所示,在长方体ABCD-A1B1C1D1中,E,F分别是棱AA1和棱CC1的中点.求证:EB1∥DF,ED∥B1F.(提示:设G是DD1的中点,分别连接EG,GC1)
如图所示,在长方体ABCD-A1B1C1D1中,E,F分别是棱AA1和棱CC1的中点.求证:EB1∥DF,ED∥B1F.(提示:设G是DD1的中点,分别连接EG,GC1) 分析 设G是DD1的中点,分别连接EG,GC1,推导出DFC1G是平行四边形,EB1C1G是平行四边形,从而DFB1E是平行四边形,由此能证明EB1∥DF,ED∥B1F.
解答 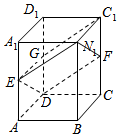 证明:设G是DD1的中点,分别连接EG,GC1
证明:设G是DD1的中点,分别连接EG,GC1
∵在长方体ABCD-A1B1C1D1中,E,F分别是棱AA1和棱CC1的中点,
∴DG$\underset{∥}{=}$FC1,∴DFC1G是平行四边形,
∴GC1$\underset{∥}{=}$DF,
又EG$\underset{∥}{=}$B1C1,∴EB1C1G是平行四边形,
∴GC1$\underset{∥}{=}$EB1,
∴EB1$\underset{∥}{=}$DF,∴DFB1E是平行四边形,
∴EB1∥DF,ED∥B1F.
点评 本题考查直线与直线平行的证明,是中档题,解题时要认真审题,注意平行公理的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 1998立方尺 | B. | 2012立方尺 | C. | 2112立方尺 | D. | 2324立方尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
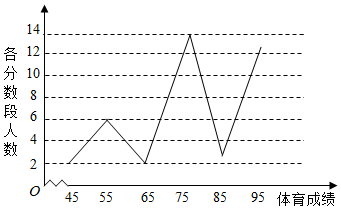
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (kπ-$\frac{π}{2}$,kπ+$\frac{π}{2}$)(k∈Z) | B. | (kπ,(k+1)π)(k∈Z) | C. | (kπ-$\frac{3π}{4}$,kπ+$\frac{π}{4}$)(k∈Z) | D. | (kπ-$\frac{π}{4}$,kπ+$\frac{3π}{4}$)(k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com